11 Amazing NumPy Shuffle Examples
Python’s NumPy package offers various methods that are used to perform operations involving randomness, such as the methods to randomly select one or more numbers from a given list of numbers, or to generate a random number in a given range, or to randomly generate a sample from a given distribution.
All these methods are offered under the random module of the NumPy package.
One such method is the numpy.random.shuffle method.
This method is used to randomly shuffle the elements of the given ‘mutable’ iterables.
Note that the reason for the iterables to be mutable is that the shuffling operation involves item re-assignment, which is not supported by immutable objects.
- 1 What are the benefits of shuffling?
- 2 How to shuffle NumPy array?
- 3 Shuffle multiple NumPy arrays together
- 4 Shuffle 2D arrays
- 5 Shuffle columns of 2D NumPy array
- 6 Shuffle multidimensional NumPy arrays
- 7 Shuffle a list
- 8 Shuffle with seed
- 9 Shuffle dimensions of NumPy array
- 10 Shuffle vs permutation
What are the benefits of shuffling?
The shuffling operation is fundamental to many applications where we want to introduce an element of chance while processing a given set of data.
It is particularly helpful in situations where we want to avoid any kind of bias to be introduced in the ordering of the data while it is being processed.
Shuffling operation is commonly used in machine learning pipelines where data are processed in batches.
Each time a batch is randomly selected from the dataset, it is preceded by a shuffling operation.
It can also be used to randomly sample items from a given set without replacement.
How to shuffle NumPy array?
Let us look at the basic usage of the np.random.shuffle method.
We will shuffle a 1-dimensional NumPy array.
import numpy as np
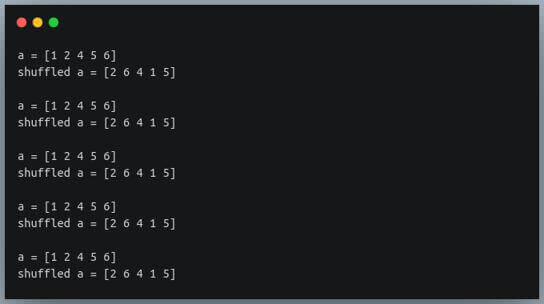
for i in range(5):
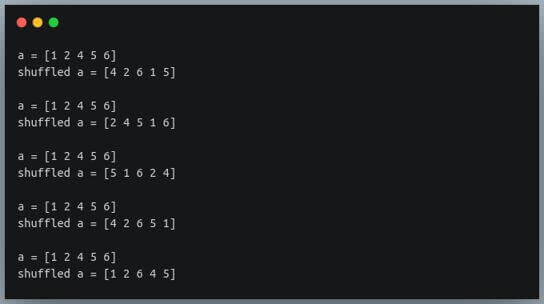
a=np.array([1,2,4,5,6])
print(f"a = {a}")
np.random.shuffle(a)
print(f"shuffled a = {a}\n")
Output:
Each time we call the shuffle method, we get a different order of the array a.
Note that the output you get when you run this code may differ from the output I got because, as we discussed, shuffle is a random operation.
In a later section, we will learn how to make these random operations deterministic to make the results reproducible.
Shuffle multiple NumPy arrays together
We saw how to shuffle a single NumPy array. Sometimes we want to shuffle multiple same-length arrays together, and in the same order.
While the shuffle method cannot accept more than 1 array, there is a way to achieve this by using another important method of the random module – np.random.permutation.
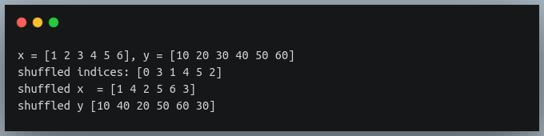
x = np.array([1,2,3,4,5,6])
y = np.array([10,20,30,40,50,60])
print(f"x = {x}, y = {y}")
shuffled_indices = np.random.permutation(len(x)) #return a permutation of the indices
print(f"shuffled indices: {shuffled_indices}")
x = x[shuffled_indices]
y = y[shuffled_indices]
print(f"shuffled x = {x}\nshuffled y {y}")
Output:
We are first generating a random permutation of the integer values in the range [0, len(x)), and then using the same to index the two arrays.
If you are looking for a method that accepts multiple arrays together and shuffles them, then there exists one in the scikit-learn package – sklearn.utils.shuffle.
This method takes as many arrays as you want to shuffle and returns the shuffled arrays.
from sklearn.utils import shuffle
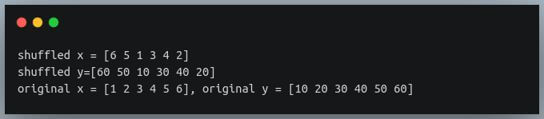
x = np.array([1,2,3,4,5,6])
y = np.array([10,20,30,40,50,60])
x_shuffled, y_shuffled = shuffle(x,y)
print(f"shuffled x = {x_shuffled}\nshuffled y={y_shuffled}")
print(f"original x = {x}, original y = {y}")
Output:
Note that this method does not perform in-place shuffling like np.random.shuffle does, instead, it returns the shuffled array without modifying the input arrays.
Since this method does not involve in-place item reassignment, we can also shuffle immutable iterables using this method.
Shuffle 2D arrays
We have seen the effect of NumPy’s shuffle method on 1-dimensional array.
Let us see what it does with 2D arrays.
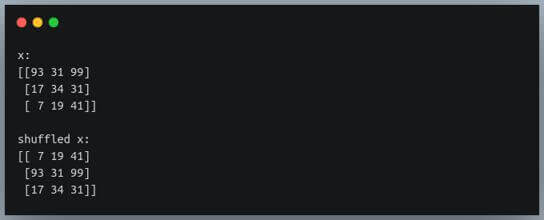
x = np.random.randint(1,100, size=(3,3))
print(f"x:\n{x}\n")
np.random.shuffle(x)
print(f"shuffled x:\n{x}")
Output:
If you look closely at the output, the order of the values in individual rows does not change; however, the positions of the rows in the array have been shuffled.
So the shuffle method shuffles the rows of a 2D array by default.
Shuffle columns of 2D NumPy array
We have seen in the last section the behavior of the shuffle method on a 2D array.
It shuffles the rows of the array in-place.
However, what do we do if we want to shuffle the columns of the array instead?
The shuffle method does not take any additional parameter to specify the axis along which we want to perform the shuffle.
So if we want to shuffle the columns of a 2D array using the np.random.shuffle method, we must find a way to treat the columns as rows or swap the columns with rows.
This is possible through transpose operation.
We will perform the shuffle on a transposed version of the 2D array, and since the shuffling occurs in-place, it will effectively shuffle the columns of the original array.
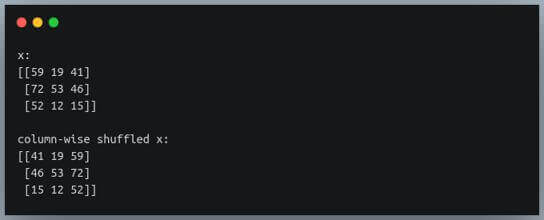
x = np.random.randint(1,100, size=(3,3))
print(f"x:\n{x}\n")
np.random.shuffle(x.T) #shuffling transposed form of x
print(f"column-wise shuffled x:\n{x}")
Output:
The columns of array x have been shuffled now, instead of the rows.
Shuffle multidimensional NumPy arrays
We have seen the behavior of the shuffle method on 1 and 2-dimensional arrays. Let us now try to understand what happens if we pass a higher dimensional array to this method.
Let us pass a 3-dimensional array to the np.random.shuffle method.
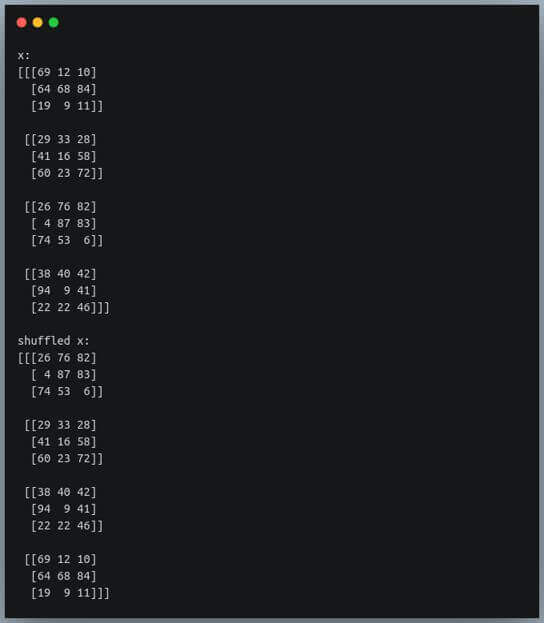
x = np.random.randint(1,100, size=(4,3,3))
print(f"x:\n{x}\n")
np.random.shuffle(x)
print(f"shuffled x:\n{x}")
Output:
Here the positions of the individual 3×3 arrays have been shuffled.
This behavior is similar to what we observed with 2-dimensional arrays.
The shuffle method, by default, shuffles any higher dimensional array along the first dimension i.e axis=0.
Shuffle along axis
If we want the array to be shuffled along any other axis, we can use the technique we discussed in the previous section.
We can generate a random permutation of the indices along that axis, and use it to index the array.
Let’s shuffle the 4x3x3 arrays along axis 1 and 2.
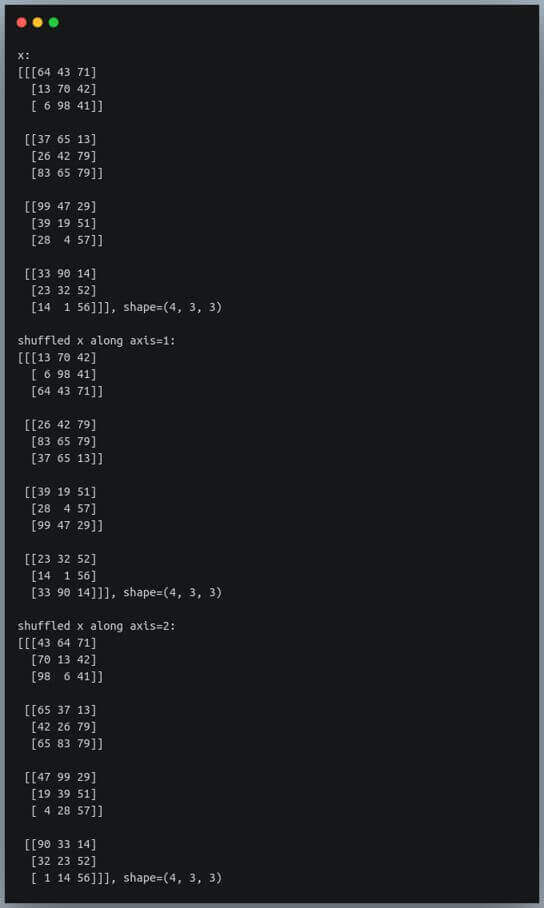
x = np.random.randint(1,100, size=(4,3,3))
print(f"x:\n{x}, shape={x.shape}\n")
indices_1 = np.random.permutation(x.shape[1])
x_1 = x[:,indices_1,:]
print(f"shuffled x along axis=1:\n{x_1}, shape={x_1.shape}\n")
indices_2 = np.random.permutation(x.shape[2])
x_2 = x[:,:,indices_2]
print(f"shuffled x along axis=2:\n{x_2}, shape={x_2.shape}\n")
Output:
In the first output, when we shuffle along axis=1, the rows of each 3×3 array have been shuffled.
Similarly, when we shuffle along axis-2, the columns of the arrays have been shuffled.
Shuffle a list
In an earlier section, we discussed one of the conditions for the np.random.shuffle method to work is that the input must be a mutable object since the method involves in-place item reassignment.
Another condition for any shuffle method to work is that the input object must be subscriptable. That means the individual elements of the input can be identified and accessed using their positions or indices.
Among the basic data structures offered by Python, the list is the only data structure that satisfies both these conditions.
Sets and Dictionaries are mutable but not subscriptable.
Tuples and Strings are subscriptable but not mutable.
Let us shuffle a Python list using the np.random.shuffle method.
a = [5.4, 10.2, "hello", 9.8, 12, "world"]
print(f"a = {a}")
np.random.shuffle(a)
print(f"shuffle a = {a}")
Output:
If we want to shuffle a string or a tuple, we can either first convert it to a list, shuffle it and then convert it back to string/tuple;
Or we can use scikit-learn’s shuffle method to get a shuffled copy of it.
Shuffle with seed
If you have been implementing the code snippets while following this blog, you must have noticed that the results you get after performing a shuffle operation differ from the results shown in the output here.
This is because the shuffle is a random operation, and hence the results are not reproducible.
The random operations in programming languages are not truly random. These operations are performed with the help of a pseudo-random number generator, which is obtained by performing a series of mathematical operations on a number called ‘seed’.
If we fix the value of seed before performing a random operation or even a series of random operations, the final output will become deterministic and can be reproduced every time using the same seed.
Let us go back to the first shuffle operation we performed in this blog.
We shuffled a NumPy array five times in a row using a for loop, and each time we got a different output.
Let us now set a fixed random seed each time before shuffling the original array, and see if we get the same output or a different one.
for i in range(5):
a=np.array([1,2,4,5,6])
print(f"a = {a}")
np.random.seed(42) #setting the random seed
np.random.shuffle(a)
print(f"shuffled a = {a}\n")
Output:
We are setting a random seed using np.random.seed() before each call to np.random.shuffle to make the shuffle operation deterministic.
However, it is not necessary to set the random seed before every call to a random operation.
If you set the random seed once before performing a series of random operations at different instances in your code; you can reproduce the output of the code later, on another day or a different machine, by setting the same seed at the beginning of the code.
Shuffle dimensions of NumPy array
We have so far performed shuffle operations on NumPy arrays without affecting the shape of the arrays.
We have been shuffling the content of the array along a chosen axis.
However, what if we want to shuffle the axes of the arrays instead of their elements?
NumPy arrays have a method called transpose, which accepts a tuple of axis indices and reshapes the array as per the order of the axes passed.
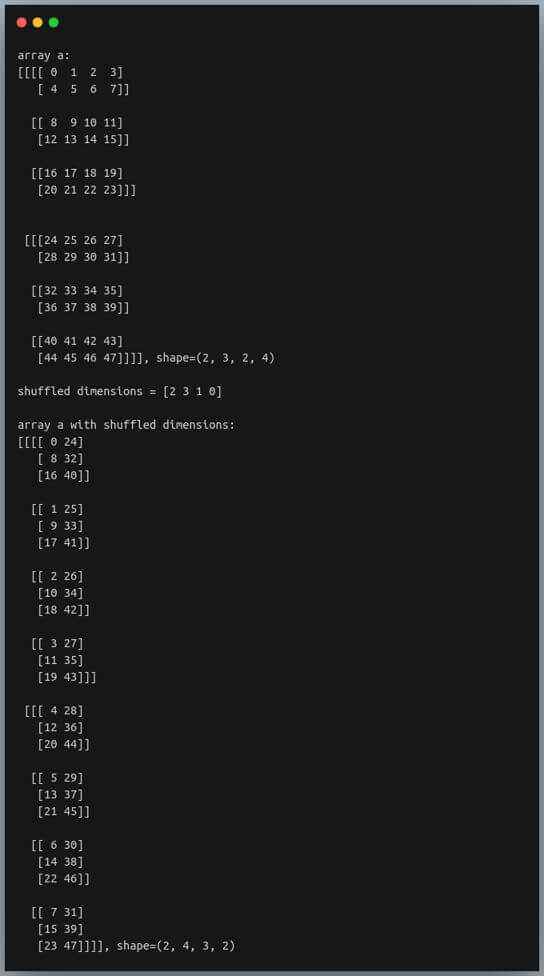
Let us build a 4-dimensional array of shape (2,3,2,4) and then shuffle its dimensions.
np.random.seed(0)
a = np.arange(48).reshape(2,3,2,4)
print(f"array a:\n{a}, shape={a.shape}\n")
shuffled_dimensions = np.random.permutation(a.ndim)
print(f"shuffled dimensions = {shuffled_dimensions}\n")
a_shuffled = a.transpose(shuffled_dimensions)
print(f"array a with shuffled dimensions:\n{a_shuffled}, shape={a_shuffled.shape}")
Output:
The original array was of the shape (2,3,2,4).
After we shuffled its dimensions, it was transformed into the shape (2,4,3,2).
Shuffle vs permutation
We have seen under multiple sections of this blog how NumPy’s permutation method can be used to perform the shuffling operation.
Not only does np.random.permutation help in shuffling arrays in ways that np.random.shuffle cannot,
But it can also achieve the same results that shuffle produces on lists and arrays.
In this section, we will learn the various similarities and differences between the two methods.
Let us first talk about the type of input that the two methods can accept.
While the shuffle method strictly accepts only subscriptable, mutable iterables; permutation, on the other hand, accepts immutable iterables and an integer, along with mutable iterables.
When you pass an integer to np.random.permutation, it returns a permutation of the range of integers from 0 up to that integer.
np.random.seed(42) print(np.random.permutation(10))
Output:
Next, let us talk about how the two methods perform the shuffling operation.
The shuffle method performs in-place shuffling on the original iterable that we pass to the method, and hence it returns None. So the original iterable ends up getting modified.
On the other hand, permutation always returns a NumPy array regardless of the input type, and so it does not modify the original input iterable.
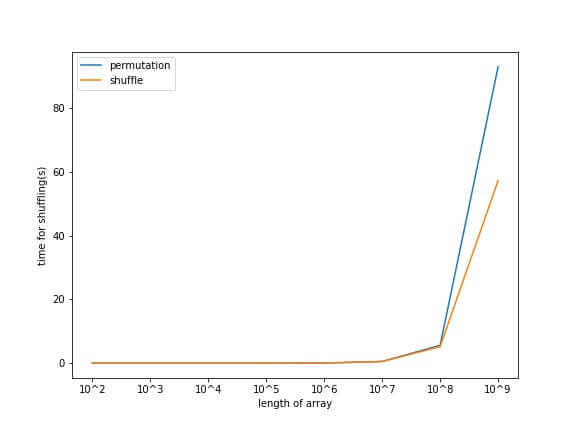
Let us also compare the time it takes for the two methods to shuffle the same array.
We will run the two methods on the same array and log the time it takes for them to shuffle it.
We will log times for arrays of lengths ranging from 102 to 109, with increments of orders of 10.
import numpy as np
import time as time
permutation_time_log = []
shuffle_time_log = []
for i in range(2,10):
print(f"shuffling array of length 10^{i}")
a = np.random.randint(100, size=(10**i))
t1 = time.time()
np.random.permutation(a)
t2 = time.time()
permutation_time_log.append(t2-t1)
t1 = time.time()
np.random.shuffle(a)
t2 = time.time()
shuffle_time_log.append(t2-t1)
del a
Note that we are deleting the array at the end of every loop to free up memory; this avoids any memory overhead during later iterations.
We have logged the time consumed by the two methods for arrays of increasing lengths.
Let us now plot them using pyplot.
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111)
ax.plot(permutation_time_log, label="permutation")
ax.plot(shuffle_time_log, label="shuffle")
ax.set_xlabel("length of array")
ax.set_ylabel("time for shuffling(s)")
ax.set_xticks(range(8))
ax.set_xticklabels([f"10^{i}" for i in range(2,10)])
ax.legend()
plt.show()
Output:
It is evident from the figure that the two methods take almost the same time for arrays up to length 108,
and the difference between their times becomes more prominent beyond this point.
For arrays of lengths higher than 108, the shuffle method performs shuffling faster than permutation,
and its performance over the latter becomes more significant with increasing lengths.
Machine Learning Engineer & Software Developer working on challenging problems in Computer Vision at IITK Research and Development center.
3+ years of coding experience in Python, 1+ years of experience in Data Science and Machine Learning.
Skills: C++, OpenCV, Pytorch, Darknet, Pandas, ReactJS, Django.