Plot 3D Hyperbolic Curves in Python using Matplotlib

In this tutorial, you’ll learn how to create various 3D hyperbolic curves using Python.

You’ll use libraries like NumPy and Matplotlib to generate and visualize these mathematical shapes.

 

 

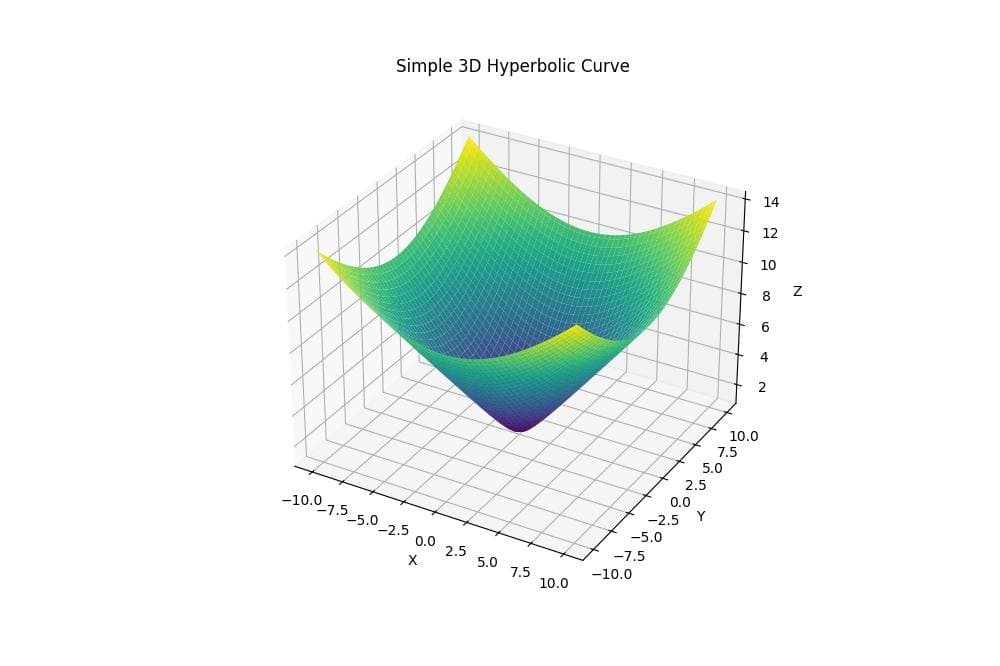
Simple 3D Hyperbolic Curve

To create a simple 3D hyperbolic curve, you can use NumPy to generate the data and Matplotlib to plot it:

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10, 10, 100)
y = np.linspace(-10, 10, 100)
X, Y = np.meshgrid(x, y)
Z = np.sqrt(1 + X**2 + Y**2)
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Simple 3D Hyperbolic Curve')
plt.show()

Output:

The Z values are calculated using the equation Z = √(1 + X² + Y²).

The resulting plot shows a smooth, upward-curving surface that extends infinitely in all directions.

 

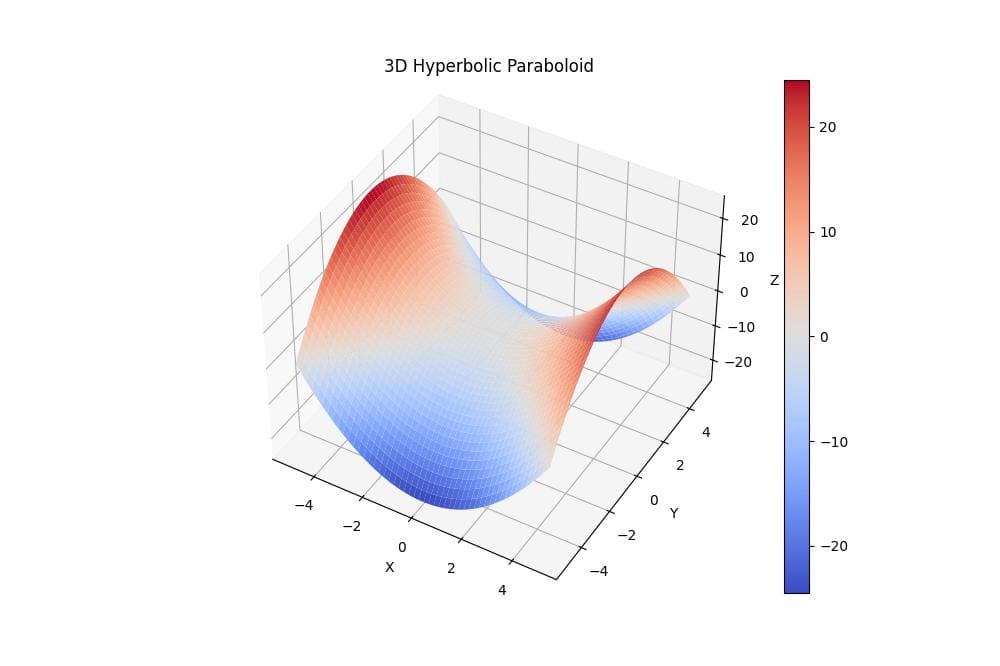
3D Hyperbolic Paraboloid

To generate a 3D hyperbolic paraboloid, you can use the following code:

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = X**2 - Y**2
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
surf = ax.plot_surface(X, Y, Z, cmap='coolwarm')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('3D Hyperbolic Paraboloid')
fig.colorbar(surf)
plt.show()

Output:

This code creates a 3D surface plot of a hyperbolic paraboloid using the equation Z = X² – Y².

The resulting plot shows a saddle-shaped surface with a central point where the curvature changes direction.

 

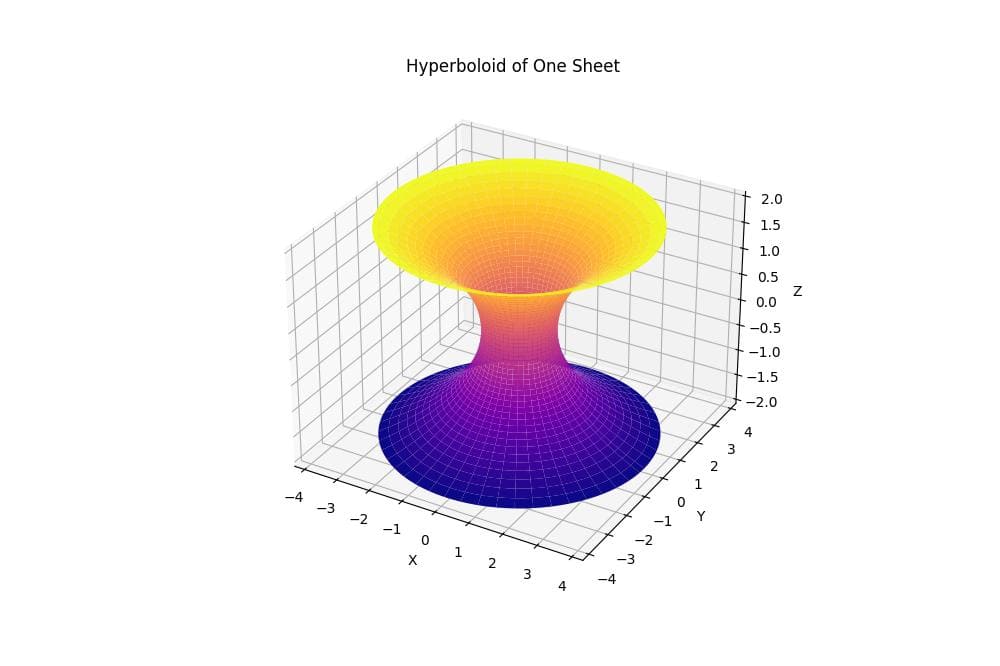
Hyperboloid of One Sheet

You can create a hyperboloid of one sheet using the following code:

import numpy as np
import matplotlib.pyplot as plt
theta = np.linspace(0, 2*np.pi, 100)
z = np.linspace(-2, 2, 100)
Theta, Z = np.meshgrid(theta, z)
X = np.cosh(Z) * np.cos(Theta)
Y = np.cosh(Z) * np.sin(Theta)
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='plasma')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Hyperboloid of One Sheet')
plt.show()

Output:

The resulting plot shows a symmetric, hourglass-shaped surface that narrows in the middle and extends outwards at both ends.

 

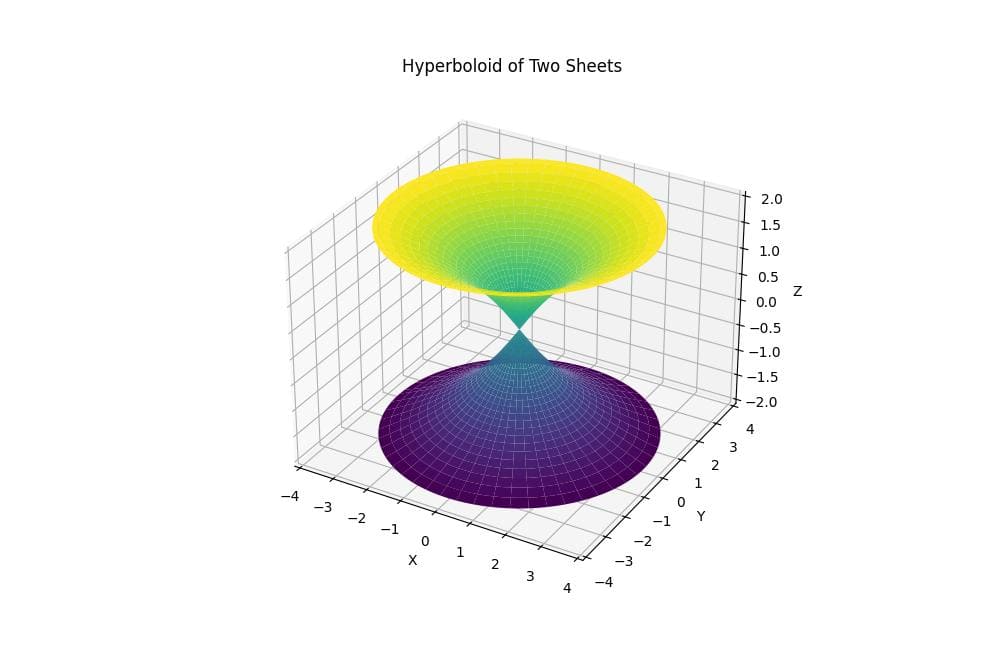
Hyperboloid of Two Sheets

To create a hyperboloid of two sheets, you can use this code:

import numpy as np
import matplotlib.pyplot as plt
theta = np.linspace(0, 2*np.pi, 100)
z = np.linspace(-2, 2, 100)
Theta, Z = np.meshgrid(theta, z)
X = np.sinh(Z) * np.cos(Theta)
Y = np.sinh(Z) * np.sin(Theta)
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Hyperboloid of Two Sheets')
plt.show()

Output:

The resulting plot shows two separate, bowl-shaped surfaces that open away from each other along the Z-axis.

 

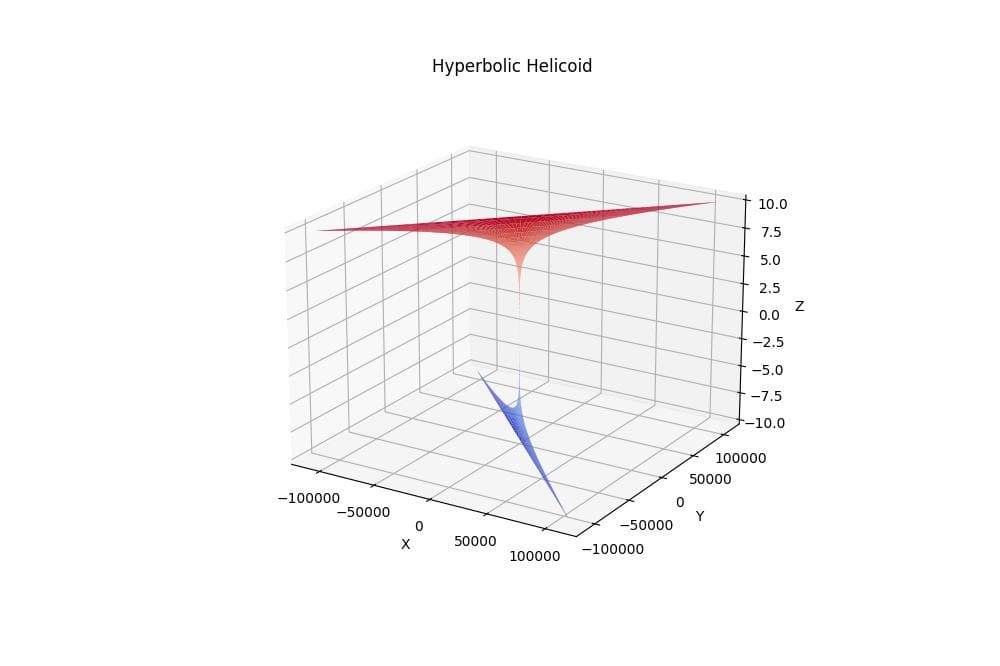
Hyperbolic Helicoid

To create a hyperbolic helicoid, you can use the following code:

import numpy as np
import matplotlib.pyplot as plt
u = np.linspace(-10, 10, 100)
v = np.linspace(-10, 10, 100)
U, V = np.meshgrid(u, v)
X = U * np.cosh(V)
Y = U * np.sinh(V)
Z = V
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='coolwarm')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Hyperbolic Helicoid')
plt.show()

Output:

The resulting plot shows a twisted surface that spirals around the Z-axis, with the curvature increasing as it moves away from the center.

 

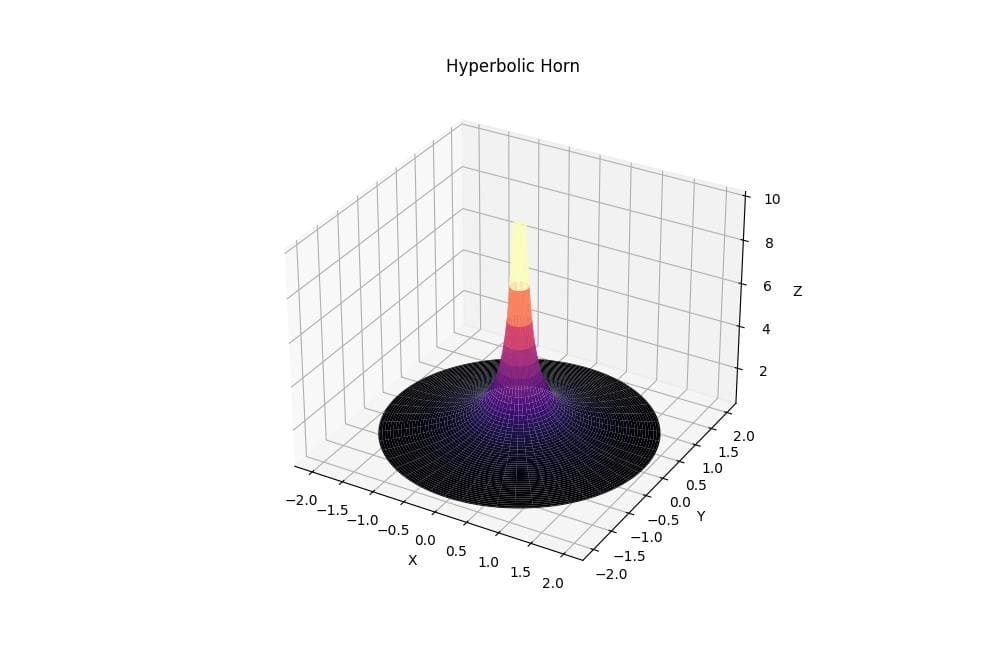
Hyperbolic Horn

To generate a hyperbolic horn, you can use this code:

import numpy as np
import matplotlib.pyplot as plt
theta = np.linspace(0, 2*np.pi, 100)
r = np.linspace(0.1, 2, 100)
Theta, R = np.meshgrid(theta, r)
X = R * np.cos(Theta)
Y = R * np.sin(Theta)
Z = 1 / R
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='magma')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Hyperbolic Horn')
plt.show()

Output:

The resulting plot shows a horn-shaped surface that starts with a wide opening and narrows rapidly as it extends along the Z-axis.