How to Shade Area Conditionally in Python Matplotlib 3D Plot

In this tutorial, you’ll learn how to conditionally shade areas in a 3D plot in Python.

This method is useful for visualizing data where certain regions need to be highlighted based on specific criteria.

 

 

To create a 3D plot, you can use the Axes3D class from Matplotlib. This class allows you to generate 3D plots and customize them.

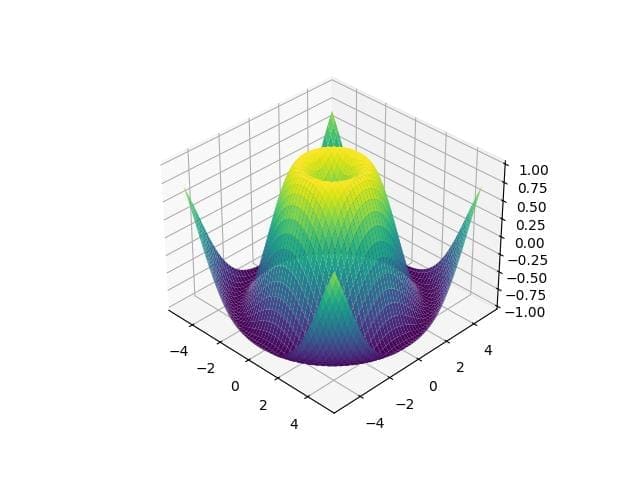
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
x, y = np.meshgrid(x, y)
z = np.sin(np.sqrt(x**2 + y**2))
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, cmap='viridis')
plt.show()

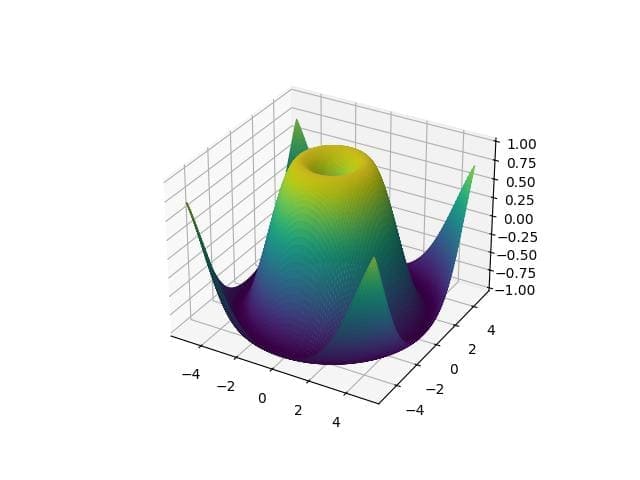
Output:

The plot displays a 3D surface of the sine function over a grid.

 

Threshold-based conditions

Shading based on Z-value

You can shade areas in a 3D plot based on a threshold Z-value using conditional logic.

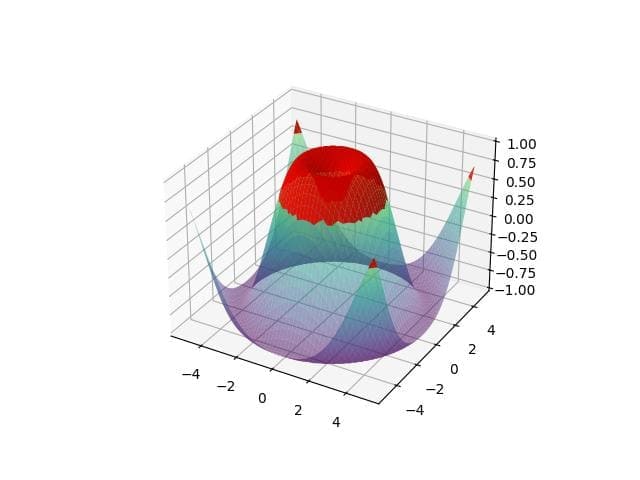
threshold = 0.5

# Create a mask for shading
z_mask = np.where(z > threshold, z, np.nan)

# Plot with shading
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, cmap='viridis', alpha=0.5)
ax.plot_surface(x, y, z_mask, color='red', alpha=0.9)
plt.show()

Output:

The plot shows the original surface with a semi-transparent overlay where the Z-values exceed the threshold. The red shading highlights these areas.

Shading Based on Distance From a Point

To shade based on distance from a specific point, calculate the distance and apply a condition.

# Define a point
point = np.array([0, 0])

# Calculate distance from the point
distance = np.sqrt((x - point[0])**2 + (y - point[1])**2)

# Define a distance threshold
distance_threshold = 4

# Create a mask for shading
distance_mask = np.where(distance < distance_threshold, z, np.nan)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, cmap='viridis', alpha=0.5)
ax.plot_surface(x, y, distance_mask, color='red', alpha=0.9)
plt.show()

Output:

The plot highlights areas within a specified distance from the origin. The blue shading indicates regions closer than the defined threshold.

 

Multiple Condition Handling

To handle multiple conditions, combine logical operations to create complex masks.

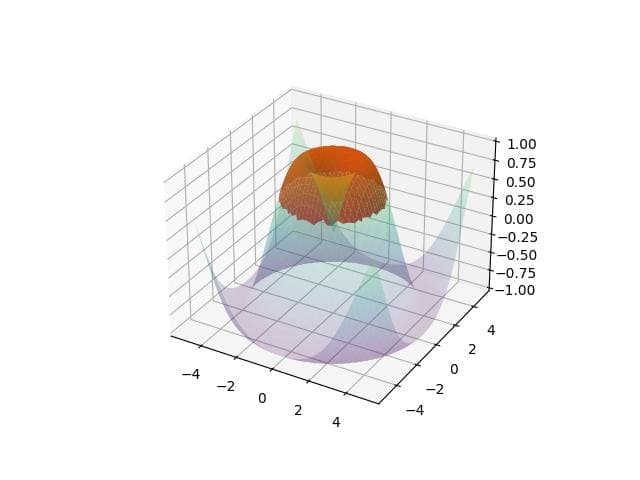
# Define multiple conditions
condition1 = z > 0.5
condition2 = distance < 3
combined_mask = np.where(condition1 & condition2, z, np.nan)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, cmap='viridis', alpha=0.2)
ax.plot_surface(x, y, combined_mask, color='red', alpha=0.9)
plt.show()

Output:

The plot shows areas where both conditions are met.

The purple shading highlights regions where the Z-value is above 0.5 and within the distance threshold.

 

Shading Multiple Regions

You can apply separate masks for each condition to shade multiple regions with distinct criteria.

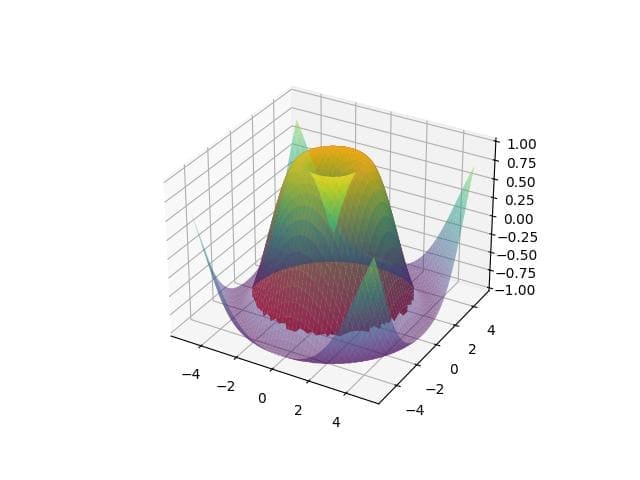
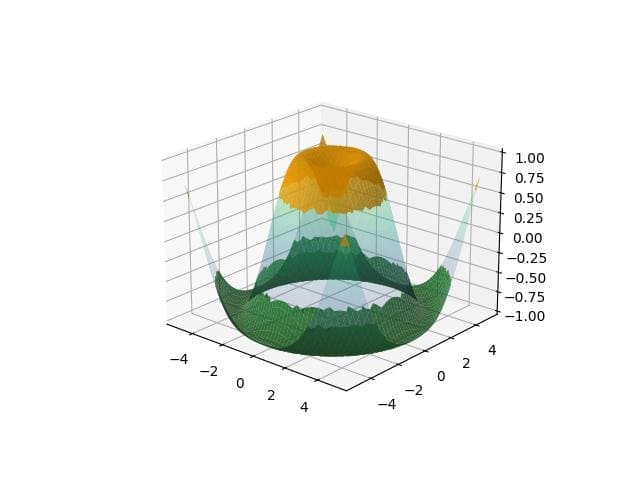
# Define another condition
condition3 = z < -0.5

# Create masks for each region
mask1 = np.where(condition1, z, np.nan)
mask2 = np.where(condition3, z, np.nan)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, cmap='viridis', alpha=0.2)
ax.plot_surface(x, y, mask1, color='orange', alpha=0.8)
ax.plot_surface(x, y, mask2, color='green', alpha=0.8)
plt.show()

Output:

The plot displays multiple shaded regions: orange for Z-values above 0.5 and green for Z-values below -0.5.

 

Gradient Shading Based on Data Values

To apply gradient shading based on data values, use a colormap to represent the range of values.

# Normalize the Z-values for gradient shading
norm = plt.Normalize(z.min(), z.max())
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, facecolors=plt.cm.viridis(norm(z)), rstride=1, cstride=1, alpha=0.9)
plt.show()

Output:

The plot uses a gradient to represent the Z-values, with colors smoothly transitioning according to the data range.