Create 3D Polar Plots in Python using Matplotlib
In this tutorial, you’ll learn how to create 3D polar plots using Python.
You’ll use the matplotlib library to visualize data in a three-dimensional polar coordinate system.
This method is useful for representing cyclical or radial data in fields like physics, engineering, and data science.
Generate Data for 3D Polar Plot
To begin, you’ll need to generate data for your 3D polar plot.
Use NumPy to create arrays for radius, theta, and phi:
import numpy as np import matplotlib.pyplot as plt r = np.linspace(0, 5, 50) theta = np.linspace(0, 2 * np.pi, 100) r, theta = np.meshgrid(r, theta) phi = np.linspace(0, np.pi, 50)
This code sets up the basic coordinate arrays for your 3D polar plot.
3D Polar Scatter Plot
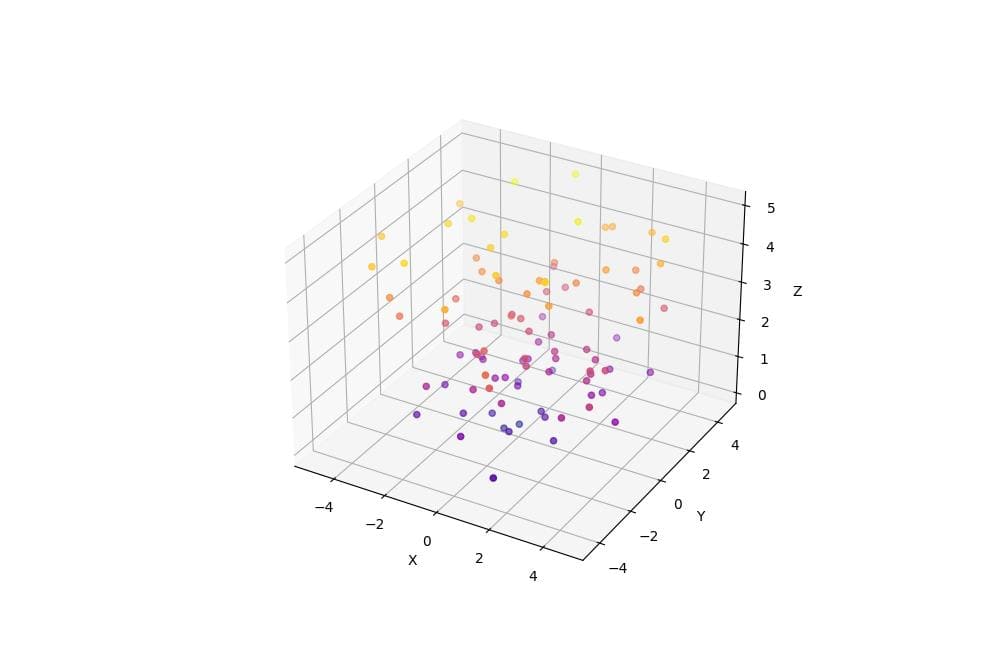
To create a 3D polar scatter plot, you can use the scatter function:
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
r = np.random.rand(100) * 5
theta = np.random.rand(100) * 2 * np.pi
z = np.random.rand(100) * 5
ax.scatter(r * np.cos(theta), r * np.sin(theta), z, c=z, cmap='plasma')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()
Output:
This code generates a 3D scatter plot with random data points in polar coordinates.
3D Polar Line Plot
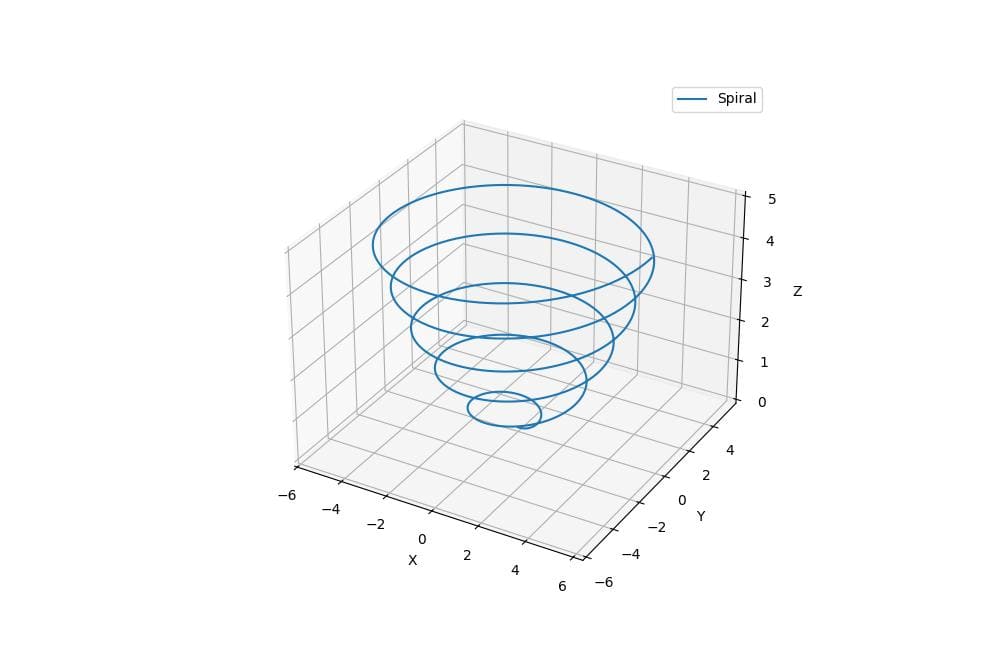
For a 3D polar line plot, you can use the plot function:
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
theta = np.linspace(0, 10 * np.pi, 1000)
r = theta ** 0.5
z = np.linspace(0, 5, 1000)
ax.plot(r * np.cos(theta), r * np.sin(theta), z, label='Spiral')
ax.legend()
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()
Output:
This code creates a 3D spiral line plot in polar coordinates.
3D Polar Surface Plot
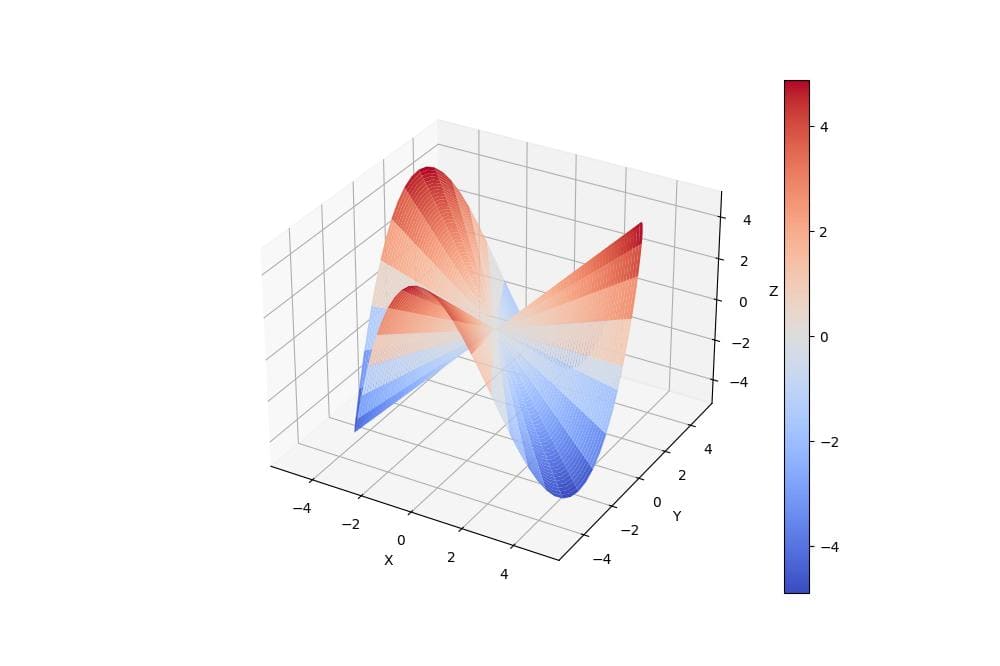
To create a 3D polar surface plot, you can use the plot_surface function:
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
r = np.linspace(0, 5, 50)
theta = np.linspace(0, 2 * np.pi, 100)
r, theta = np.meshgrid(r, theta)
z = r * np.sin(3 * theta)
surf = ax.plot_surface(r * np.cos(theta), r * np.sin(theta), z, cmap='coolwarm')
fig.colorbar(surf)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()
Output:
This code generates a 3D surface plot with a colorbar representing the z-values.
3D Polar Contour Plot
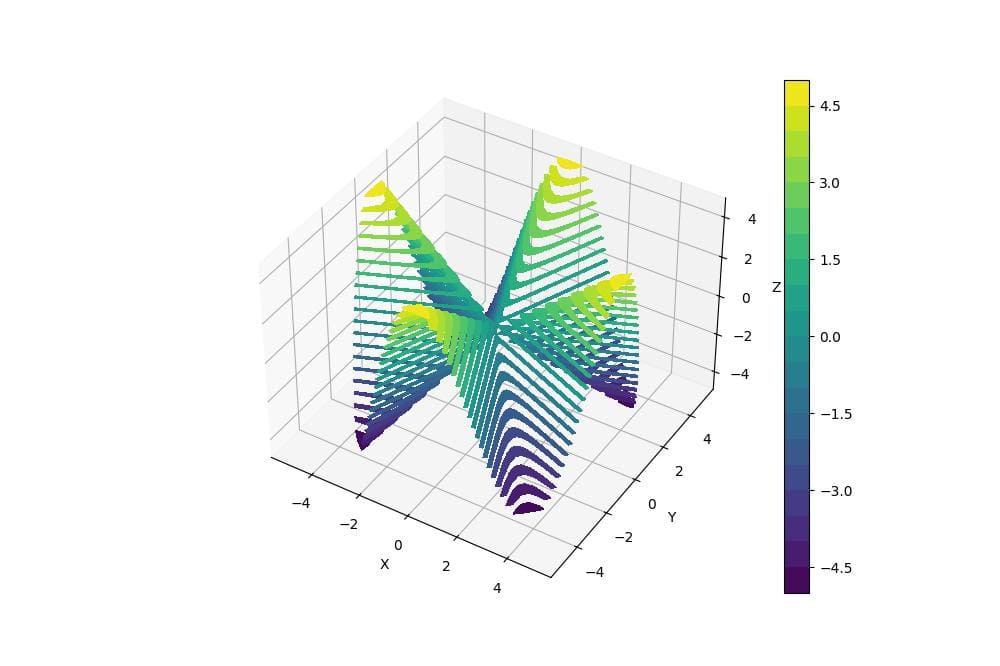
For a 3D polar contour plot, you can use the contourf function:
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
r = np.linspace(0, 5, 50)
theta = np.linspace(0, 2 * np.pi, 100)
r, theta = np.meshgrid(r, theta)
z = r * np.cos(4 * theta)
contour = ax.contourf(r * np.cos(theta), r * np.sin(theta), z, cmap='viridis', levels=20)
fig.colorbar(contour)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()
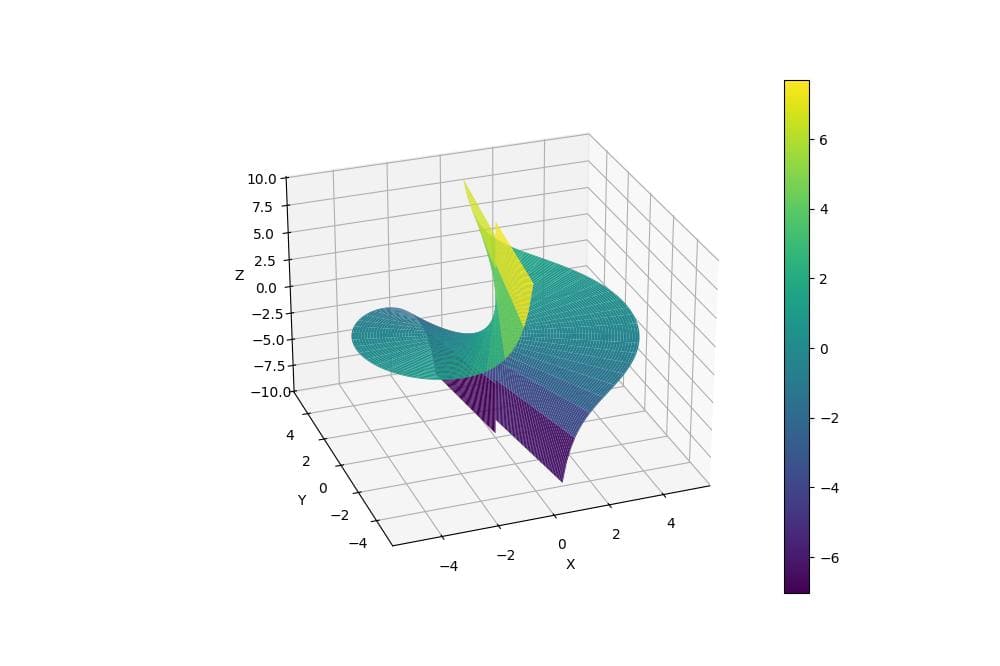
Output:
This code creates a 3D contour plot with filled contours representing the z-values.
Discontinuities in Polar Functions
To handle discontinuities in polar functions, you can use masked arrays:
import numpy.ma as ma
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
r = np.linspace(0, 5, 100)
theta = np.linspace(0, 2 * np.pi, 200)
r, theta = np.meshgrid(r, theta)
z = np.tan(theta)
z_masked = ma.masked_where(np.abs(z) > 10, z)
surf = ax.plot_surface(r * np.cos(theta), r * np.sin(theta), z_masked, cmap='viridis')
fig.colorbar(surf)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()
Output:
This code masks values where the tangent function approaches infinity.
Plot Periodic Functions
To plot periodic functions, ensure your theta range covers multiple periods:
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
r = np.linspace(0, 5, 50)
theta = np.linspace(0, 4 * np.pi, 200)
r, theta = np.meshgrid(r, theta)
z = r * np.sin(3 * theta)
surf = ax.plot_surface(r * np.cos(theta), r * np.sin(theta), z, cmap='coolwarm')
fig.colorbar(surf)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()
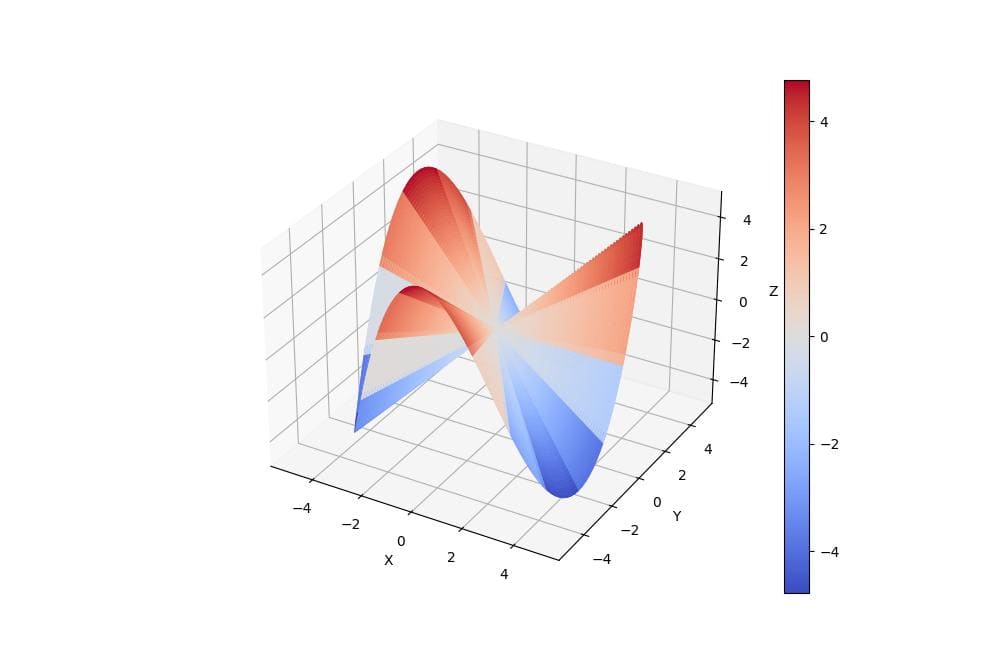
Output:
This code plots a periodic function over multiple cycles that shows its repeating nature in 3D space.
Mokhtar is the founder of LikeGeeks.com. He is a seasoned technologist and accomplished author, with expertise in Linux system administration and Python development. Since 2010, Mokhtar has built an impressive career, transitioning from system administration to Python development in 2015. His work spans large corporations to freelance clients around the globe. Alongside his technical work, Mokhtar has authored some insightful books in his field. Known for his innovative solutions, meticulous attention to detail, and high-quality work, Mokhtar continually seeks new challenges within the dynamic field of technology.