Plot Sigmoid Function in 3D Using Python

In this tutorial, you’ll learn how to plot the sigmoid function in 3D using various Python libraries.

The sigmoid function is a popular activation function in machine learning and neural networks.

Visualizing it in 3D provides valuable insights into its behavior across different input ranges.

 

 

Using Matplotlib

You can use it to create a 3D plot of the sigmoid function.

To create the 3D mesh plot, you can use the plot_surface function from Matplotlib:

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def sigmoid(x):
    return 1 / (1 + np.exp(-x))
x = np.linspace(-6, 6, 30)
y = np.linspace(-6, 6, 30)
X, Y = np.meshgrid(x, y)
Z = sigmoid(X + Y)
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
surf = ax.plot_surface(X, Y, Z, cmap='viridis')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
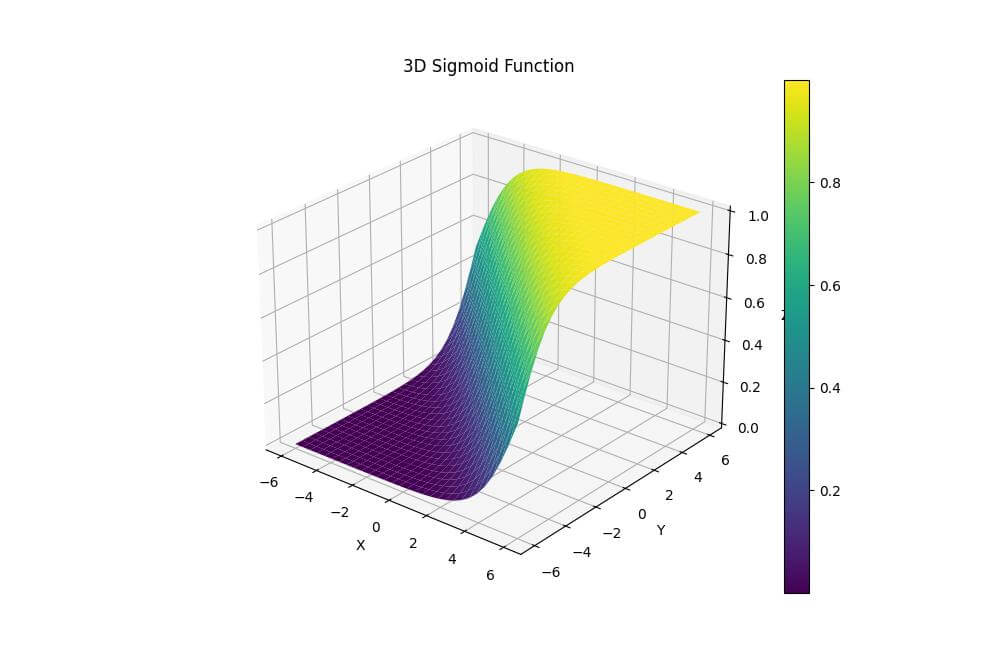
ax.set_title('3D Sigmoid Function')
fig.colorbar(surf)
plt.show()

Output:

The X and Y axes represent the input values, while the Z-axis shows the output of the sigmoid function.

The colorbar on the right indicates the range of values in the plot.

 

Using Plotly

You can create an engaging visualization of the sigmoid function using Plotly:

import numpy as np
import plotly.graph_objects as go
def sigmoid(x):
    return 1 / (1 + np.exp(-x))
x = np.linspace(-6, 6, 50)
y = np.linspace(-6, 6, 50)
X, Y = np.meshgrid(x, y)
Z = sigmoid(X + Y)
fig = go.Figure(data=[go.Surface(z=Z, x=X, y=Y)])
fig.update_layout(title='3D Sigmoid Function', autosize=False,
                  width=800, height=600,
                  scene=dict(xaxis_title='X', yaxis_title='Y', zaxis_title='Z'))
fig.show()

Output:

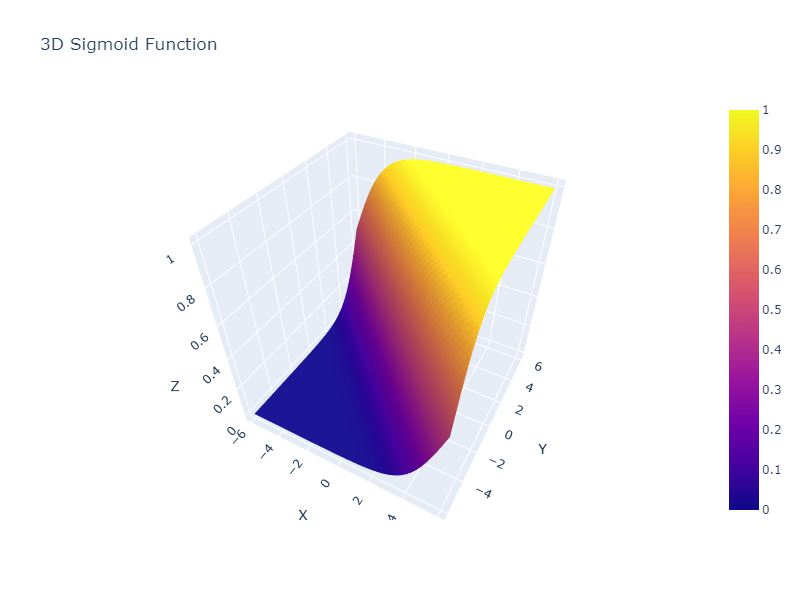
You can rotate, zoom, and pan the plot to explore different aspects of the sigmoid function.

The color gradient represents the range of values in the Z-axis.

 

Wireframe Plot Representation

You can combine numpy and mpl_toolkits to create a 3D wireframe plot of the sigmoid function:

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def sigmoid(x):
    return 1 / (1 + np.exp(-x))
x = np.linspace(-6, 6, 30)
y = np.linspace(-6, 6, 30)
X, Y = np.meshgrid(x, y)
Z = sigmoid(X + Y)
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
ax.plot_wireframe(X, Y, Z, rstride=2, cstride=2)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
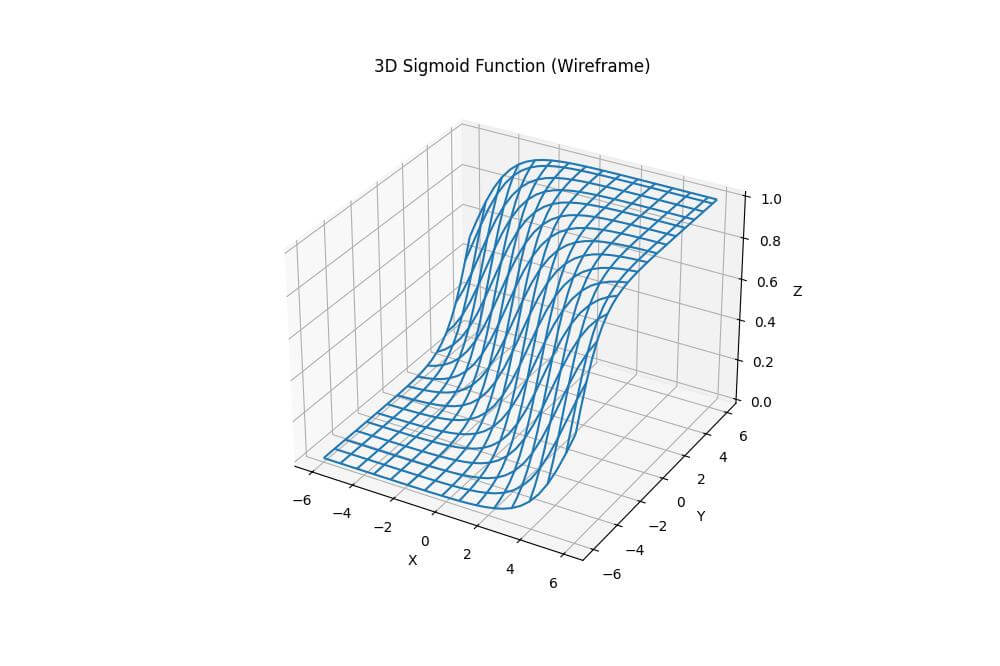
ax.set_title('3D Sigmoid Function (Wireframe)')
plt.show()

Output:

The wireframe representation allows you to see through the surface.

The rstride and cstride parameters control the density of the wireframe.