Python math functions (Simple Examples)

In this tutorial, you will learn about Python math functions in the math module of Python. Mathematical calculations are always required in any type of project.

In Python, some built-in math operators do not require the math module such as addition, subtraction, multiplication, division.
Advanced operations such as trigonometric (sin, cos, etc.), logarithmic, exponential, or factorial, etc. are not built-in. That’s why the math module is imported.

 

 

Math constants

In addition to the advanced mathematical operations, the math module also provides predefined mathematical constants that are:

• Pi (math.pi)
• Euler’s number (math.e)
• Tau (math.tau)
• Infinity (math.inf)
• Not a number (math.nan)

 

Pi

Pi is a mathematical constant defined as the ratio of the circumference of a circle to the diameter of the circle.
Π = c/d
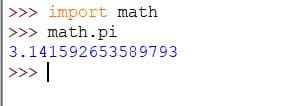
Where c is the circumference of the circle and d is the diameter of the circle. The value of pi is 3.14. Pi (Π) can be accessed in Python as:

Code:

import math
math.pi
#3.141592653589793

Output:

Consider the following example where we used pi to find the circumference of a circle:

Code:

import math
radius = 5
circumference = 2 * math.pi * radius
print ("Circumference of circle = ", circumference)

Output:

Euler’s Number (e)

Euler’s number is the base of the natural logarithm. It is denoted by symbol e. The value of e is approximated to be 2.718. Euler’s number can be accessed in Python as follows:

Code:

import math
math.e
#2.718281828459045

Output:

Tau

Tau (𝜏) is a mathematical constant, defined as the ratio of the circumference of the circle to the radius of the circle.

math.tau = 2*pi

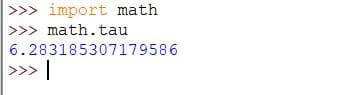
Check out the code below:

 

Code:

import math
math.tau
#6.283185307179586

Output:

Infinity

Infinity is a boundless entity that cannot be defined in numbers. In Python, positive and negative infinities are defined as follows:

Code:

import math
math.inf
-math.inf

Output:

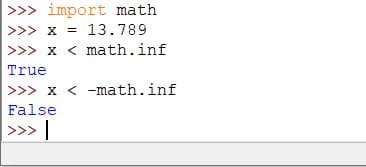
Infinity is used to compare given numbers to the absolute maximum and absolute minimum values as demonstrated in the code below:

Code:

import math
x = 13.789
x < math.inf
x < -math.inf

Output:

 

Not a number (nan)

Not a number (nan) refers to non-numerical values. Not a number (nan) makes sure that the value of a given numerical variable is a number.

Code:

import math
math.nan

Output:

 

floor()

The floor() method of the math module rounds down a number to the nearest integer. Syntax for floor() is given below:

Syntax:

math.floor(x)

• x is the input number. The floor() method takes positive or negative numbers as input.

The floor() method returns the nearest integer less than or equal to x. If the number is a floating-point number, 10.89, floor() will return 10.

If the number is an integer, floor() will return the same integer. Consider the following example:

Code:

import math
x = 3.5367
math.floor(x)
x = 6
math.floor(x)

Output:

 

ceil()

The ceil() method of the math module rounds up a number to the nearest integer. Syntax for ceil() is given below:

Syntax:

math.ceil(x)

• x is the input number. The ceil() method takes positive or negative numbers as input.

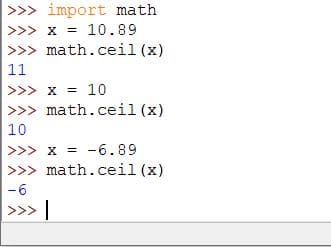
The ceil() method returns an integer value greater than or equal to x. If the number is a floating-point number, 10.89, ceil() will return 11.

If the number is an integer, ceil() will return the same integer. The following example explains the ceil() method:

 

Code:

import math
x = 10.89
math.ceil(x)
x = 10
math.ceil(x)

Output:

 

trunc()

import math
num = 3.721
result = math.trunc(num)
print(result)

Output

3

math.trunc() is a function that removes the fractional part of any number and returns its integer part. In this case, num was 3.721, and after applying math.trunc(num), we got 3, which is the integer part of the number.

 

copysign()

import math
x = -10
y = 15
result = math.copysign(x, y)
print(result)

Output

10.0

math.copysign(x, y) is a function that returns the magnitude of x but with the sign of y.

In our case, x was -10 (so, the magnitude is 10), and y was 15 which is positive. Therefore, the result is a positive 10.

 

modf()

import math
num = 3.721
result = math.modf(num)
print(result)

Output

(0.7210000000000001, 3.0)

math.modf(x) returns a tuple representing the fractional and integer parts of x. The fractional part is returned as the first item of the tuple and the integer part as the second.

In our example, num was 3.721 and math.modf(num) returned (0.7210000000000001, 3.0).

The fractional part 0.721 and the integer part 3.0 correspond to the parts of num.

 

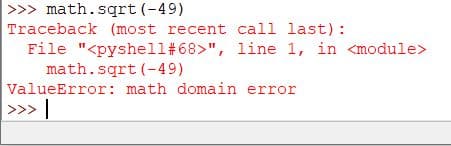
sqrt()

The sqrt() method returns the square root of an input value. The syntax of sqrt() is as follows:

Syntax:

math.sqrt(x)

• x is the input number. It must be greater than or equal to 0. If x is less than 0 (negative number), sqrt() will return ValueError.

The sqrt() method returns a floating-point number. Consider the example below:

Code:

import math
math.sqrt(9)
math.sqrt(4)
math.sqrt(24)
math.sqrt(-49)

Output:

If the number is less than 0, we will have the following error:

 

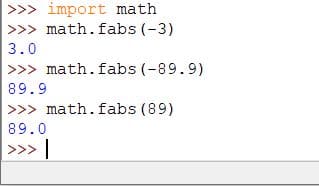
fabs(x)

fabs represents the absolute function. The absolute function returns a non-negative value of the given number.
It means that the absolute value of a positive number will be the same number and if the given number is negative, the fabs function will convert it into a positive number.
For example, the fabs value of -8 will be 8 and the fabs value of 8 will be 8. Syntax of fabs is given below:

Syntax:

math.fabs(x)

• x can be an integer or a floating-point.

The method will return a non-negative floating-point number. Consider the following example:

Code:

import math
math.fabs(-3)
math.fabs(-89.9)
math.fabs(89)

Output:

The difference between math.fabs() method and the python’s abs() method is that the math.fabs() method always returns a floating-point number.

 

pow(x)

The pow() method of the math module returns the value of input number x raised to the power y that is x^y.
The syntax for math.pow() is as follows:

Syntax:

math.pow(x, y)

• x is the input number and y is the power of x. If x is 3 and y equals 4, it will mean: 3^{4 = 3 * 3 * 3 * 3.}

The function returns a floating-point value.
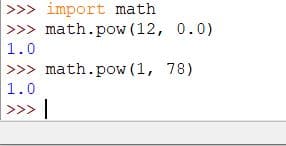
In mathematics, anything raised to power 0 equals 1, and 1 raised to power anything also equals 1. Therefore, the pow() method will return 1.0 if y is 0 and x is any number.

Similarly, pow() will return 1.0 if x is 1 and y is any number.

math.pow(x, 0.0) = 1.0
math.pow(1.0, y) = 1.0

Output:

Code:

import math
print("3 raised to power 4 = ", math.pow(3, 4))

Output:

 

isclose()

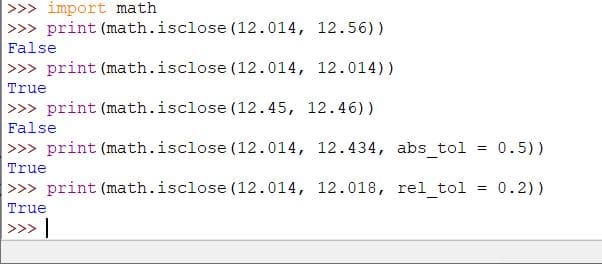
The isclose() method of the math module uses relative and absolute tolerance to check the closeness of two values.

Tolerance is defined as the threshold to check the closeness of the numbers.
If the two numbers are close to each other, the isclose() method will return true and return false if they are not close to each other.
The syntax of isclose() is given below:

Syntax:

math.isclose(a, b, rel_tol, abs_tol)

• a and b are the numbers to check the closeness of.
• rel_tol (optional) is the relative tolerance and is defined as the maximum difference between the input values (a and b). The default value of rel_tol is: 1e-09 or 0.000000001. rel_tol should be greater than 0.
• abs_tol (optional) is the minimum absolute tolerance. abs_tol compares values nearer to 0. abs_tol should be at least 0.

The math.isclose() method returns Boolean value:

• True if the given numbers are close.
• False if the given numbers are not close.

Check out the code below:

Code:

import math
print(math.isclose(12.014, 12.56))
print(math.isclose(12.014, 12.014))
print(math.isclose(12.45, 12.46))
print(math.isclose(12.014, 12.434, abs_tol = 0.5))
print(math.isclose(12.014, 12.018, rel_tol = 0.2))

Output:

 

isfinite()

import math
num = 10/3
result = math.isfinite(num)
print(result)

Output

True

The math.isfinite(x) function checks if x is a finite number. In this case, num was 10/3, which is a finite number, so math.isfinite(num) returns True.

 

isinf()

import math
num = math.inf
result = math.isinf(num)
print(result)

Output

True

math.isinf(x) checks if x is a positive or negative infinity. Here, num is math.inf, which is positive infinity, so math.isinf(num) returns True.

 

isnan()

import math
num = math.nan
result = math.isnan(num)
print(result)

Output

True

math.isnan(x) checks if x is a NaN (not a number). In our case, num is math.nan, which is a NaN, hence math.isnan(num) returns True.

 

nextafter()

import math
x = 1.0
y = 2.0
result = math.nextafter(x, y)
print(result)

Output

1.0000000000000002

The math.nextafter(x, y) function returns the next representable floating-point value after x in the direction towards y.

If x equals y, then y is returned. In our case, math.nextafter(1.0, 2.0) returned 1.0000000000000002 as the closest representable float value after 1.0 towards 2.0.

 

remainder()

import math
x = 10
y = 3
result = math.remainder(x, y)
print(result)

Output

1.0

The math.remainder(x, y) function computes the IEEE 754-style remainder of x with respect to y. In simple terms, it returns the rest of the division of x by y.

In our case, math.remainder(10, 3) returned 1.0 because 1 is the remainder when 10 is divided by 3.

 

ulp()

import math
x = 1.0
result = math.ulp(x)
print(result)

Output

2.220446049250313e-16

math.ulp(x) returns the value of the unit in the last place (ULP) of x. It’s the difference between x and the nearest representable floating-point number.

Here, math.ulp(1.0) returned 2.220446049250313e-16, which is the difference between 1.0 and the next closest representable floating-point value.

 

frexp()

import math
x = 14.0
result = math.frexp(x)
print(result)

Output

(0.875, 4)

math.frexp(x) returns a tuple containing the mantissa and exponent of x as per the representation x = m * 2**exp.

Here, math.frexp(14.0) returned (0.875, 4) since 14.0 can be represented as 0.875 * 2**4.

 

ldexp()

import math
m = 0.875
exp = 4
result = math.ldexp(m, exp)
print(result)

Output

14.0

math.ldexp(m, exp) is a function that calculates m * (2**exp). In our case, m was 0.875 and exp was 4. Therefore, the result is 14.0, because 0.875 * (2**4) equals 14.0.

 

factorial()

The factorial() method of the math module returns the factorial of the given number. The input number must be a positive number.
Factorial of a number is the multiplication of numbers starting from the input number back to 1.

Syntax:

math.factorial(x)

• x should be a positive integer. If x is non-integer or negative, you will get a ValueError.

The math.factorial() method returns a positive int value. The following code uses math.factorial():

Code:

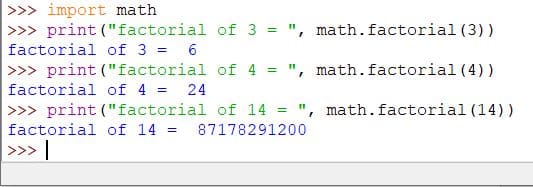
import math
print("factorial of 3 = ", math.factorial(3))
print("factorial of 4 = ", math.factorial(4))
print("factorial of 14 = ", math.factorial(14))

Output:

 

prod()

The prod() method of the math module works on iterables. It returns the product of all elements in an iterable or sequence. The syntax of the math.prod() method is as follows:

Syntax:

math.prod(iterable, start)

• iterable is the input sequence. The elements of the iterable must be numeric.
• start is the starting value of the product. The default value of start is 1.

If the iterable is empty, prod() will return the start value. math.prod() is used in the code below:

Code:

import math
my_list = [2, 3, 7, 6]
print("Product of elements of my list = ", math.prod(my_list))

Output:

If the iterable is empty:

Code:

my_list = []
print("Product of elements of my list = ", math.prod(my_list))

Output:

Note that math.prod() is not defined in the versions older than 3.8.

 

fsum()

The fsum() method is used to find the sum of the elements of an iterable. The syntax for math.fsum() method is as follows:

Syntax:

math.fsum(iterable)

• iterable is the input sequence.

The fsum() method returns an accurate floating-point number after calculating the sum of elements.

Code:

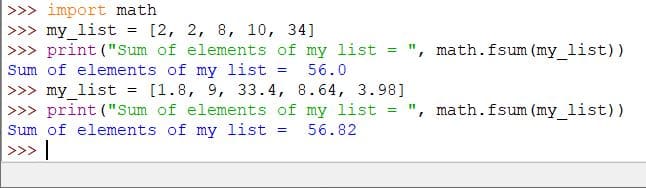
import math
my_list = [2, 2, 8, 10, 34]
print("Sum of elements of my list = ", math.fsum(my_list))
my_list = [1.8, 9, 33.4, 8.64, 3.98]
print("Sum of elements of my list = ", math.fsum(my_list))

Output:

 

dist()

import math
p = (1, 2)
q = (4, 6)
result = math.dist(p, q)
print(result)

Output

5.0

The math.dist(p, q) function calculates the Euclidean distance between two points p and q where p and q are the coordinates of two points.

In our case, p was (1,2) and q was (4,6). The Euclidean distance between these points is 5.0.

 

hypot()

import math
x = 3
y = 4
result = math.hypot(x, y)
print(result)

Output

5.0

math.hypot(x, y) calculates the Euclidean norm, sqrt(x*x + y*y). This is the length of the vector from the origin to the point (x, y).

It is used to calculate the length of the hypotenuse of a right triangle. In our example, math.hypot(3, 4) returns 5.0, which is the hypotenuse of a right triangle with other two sides of lengths 3 and 4.

 

fmod()

The fmod() method of the math module calculates the modulo of the given numbers. Modulo means, it returns the remainder of x/y.

Syntax:

math.fmod(x, y)

• x is the numerator in the fraction x/y
• y is the denominator in the fraction x/y
• x and y can be negative or positive but they must be numbers.
• If x and y, both are 0, you will get an error.
• If y = 0, you will get an error.

The fmod() method returns a floating-point value. Consider the following example:

Code:

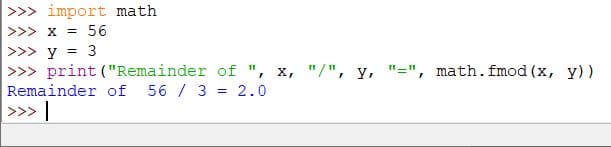
import math
x = 56
y = 3
print("Remainder of ", x, "/", "y =", math.fmod(x, y))

Output:

 

log()

The log() method of the math module calculates the natural logarithm of the input value.
The math.log() method can have 1 or 2 arguments:

• If the method has 1 argument x, the log is calculated as x log to the base e.
• If the method has 2 arguments x and y, the log is calculated as x log to the base y.

The syntax of math.log() is as follows:

Syntax:

math.log(x, y)

• x is the number to calculate the natural logarithm of. x must be greater than 0.
• If x is a negative number or 0, you will get ValueError.
• If x is not a number, you will get TypeError.
• y is optional. y is the base. If y is not specified, the default base will be e.

The log() method returns a floating-point value.

Code:

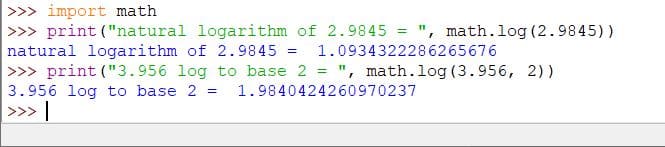
import math
print("natural logarithm of 2.9845 = ", math.log(2.9845))
print("3.956 log to base 2 = ", math.log(3.956, 2))

Output:

 

log10()

The log10() method calculates the logarithm of the input number to the base 10.

Syntax:

math.log10(x)

• x is the input number to find the logarithm of. x should be greater than 0.

The math.log10() method will return a floating-point value after calculating the base-10 logarithm.

Code:

import math
print("Log of 24.89 to the base 10 = ", math.log(24.89))

Output:

 

exp()

The method math.exp() will return E raised to power x. Here E is the base of the natural logarithm approximately equals 2.718282.

Syntax:

math.exp(x)

• x is the exponent of E.

The method math.exp() will return floating-point value from E^x.

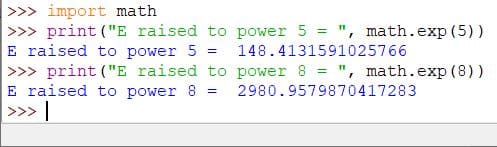
Code:

import math
print("E raised to power 5 = ", math.exp(5))
print("E raised to power 8 = ", math.exp(8))

Output:

 

erf()

The math.erf() method of the math module finds the error function of the input number. The syntax of math.erf() is given below:

Syntax:

math.erf(x)

• x is the input number to find the error function. x should be within the range of -infinity to +infinity.

The math.erf() method returns a floating-point value ranging from -1 to +1. Consider the following example:

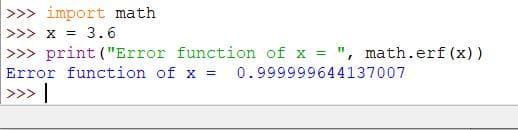
Code:

import math
x = 3.6
print("Error function of x = ", math.erf(x))

Output:

 

 

gamma()

import math
num = 5
result = math.gamma(num)
print(result)

Output

24.0

math.gamma(x) returns the Gamma function at x. The gamma of n is equivalent to the factorial of n-1. In our case, math.gamma(5) returns 24.0, which is the factorial of 4.

 

lgamma()

import math
num = 5
result = math.lgamma(num)
print(result)

Output

3.178053830347945

math.lgamma(x) returns the natural logarithm of the absolute value of the Gamma function at x.

In our example, math.lgamma(5) returns 3.178053830347945, which is the natural logarithm of the absolute value of Gamma(5).

 

gcd() (Greatest Common Divisor)

The math.gcd() method of the math module calculates the greatest common divisor of two input numbers of data type int.

Syntax:

math.gcd(x, y)

• x and y are the input numbers. Both x and y should be of data type int.
• floating-point numbers are not allowed in the gcd() method.

The math.gcd() method will return an int type value after finding the greatest common divisor of x and y. If both input numbers are 0, math.gcd() will return 0. Empty gcd() also returns 0.
GCD is the greatest common divisor that divides two input numbers and does not return any remainder value. Consider the code example below:

Code:

import math
x = 44
y = 16

print("Greatest common divisor of ", x, " and ", y, " = ", math.gcd(x, y))

Output:

 

comb()

import math
n = 5
k = 3
result = math.comb(n, k)
print(result)

Output

10

The math.comb(n, k) function calculates the number of ways to choose k items from n items without repetition and without order (this is also known as combinations in mathematics).

In our example, we calculated the combinations of 5 items taken 3 at a time, and the result is 10.

 

perm()

import math
n = 5
k = 3
result = math.perm(n, k)
print(result)

Output

60

math.perm(n, k) returns the number of ways to choose k items from n items with regard to the order (also known as permutations).

In our case, math.perm(5, 3) returns 60, which means there are 60 different ways to arrange 3 items chosen from 5.

 

lcm()

import math
num1 = 12
num2 = 20
result = math.lcm(num1, num2)
print(result)

Output

60

The function math.lcm(num1, num2) computes the least common multiple (LCM) of two numbers. The LCM of two numbers is the smallest positive integer that is perfectly divisible by both numbers. Here, math.lcm(12, 20) returns 60, which is the smallest number that both 12 and 20 can divide into evenly.

 

isqrt()

import math
num = 17
result = math.isqrt(num)
print(result)

Output

4

The function math.isqrt(num) calculates the integer square root of a number. This is the largest integer less than or equal to the square root of the number.

In our example, math.isqrt(17) returns 4 because 4 is the largest integer whose square is less than or equal to 17.

 

Angular Conversion Methods

In the Python math module, there are two helper functions to manipulate angles:

• math.degrees()
• math.radians()

math.degrees

The math.degrees() method is used to convert the given angle from radians to degrees.

Syntax:

math.degrees(x)

• x is the given angle that is to be converted from radians to degrees

The method returns a floating-point value that represents the angle in degrees.

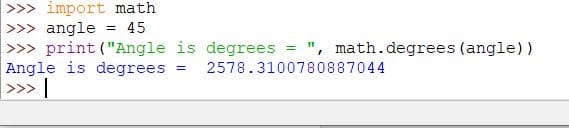
Code:

import math
angle = 45
print("Angle is degrees = ", math.degrees(angle))

Output:

math.radians

The math.radians() method converts the given angle from degrees to radians.

Syntax:

math.radians(x)

• x is the given angle that is to be converted from degrees to radians

The method returns a floating-point value that represents the angle in radians.

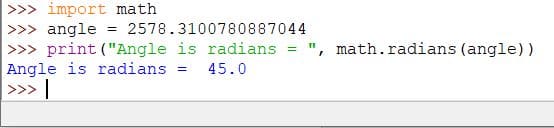
Code:

import math
angle = 2578.3100780887044
print("Angle is radians = ", math.radians(angle))

Output:

 

Trigonometric Methods

The following functions are defined in the math module to perform trigonometric operations:

sin()

The sin() method of the math module returns the sine of the given angle.

Syntax:

math.sin(x)

• x is the input angle. x must be a number.

The sin() method returns a floating-point value ranging from -1 to 1. If the input value is given in degrees, it must be converted to radians.

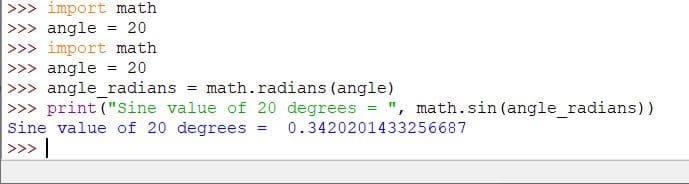
Code:

import math
angle = 20
angle_radians = math.radians(angle)
print("Sine value of 20 degrees = ", math.sin(angle_radians))

Output:

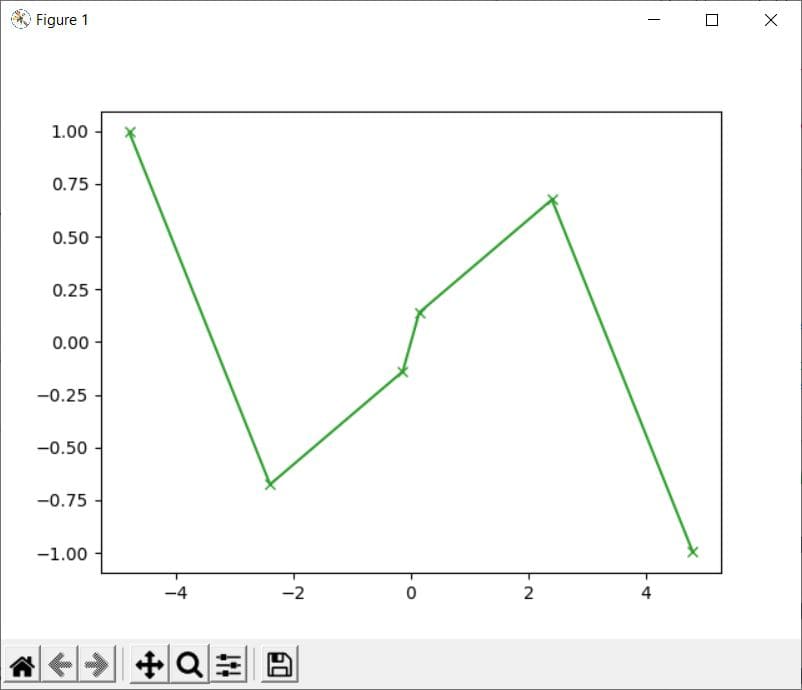
Consider the following example in which we will plot the values from sin() method using pyplot:

Code:

import math
import matplotlib.pyplot as plt
x = [-4.8, -2.4, -0.14, 0.14, 2.4, 4.8]
y = []
for i in range(len(x)):
	y.append(math.sin(x[i]))
plt.plot(x, y, marker = “x”)
plt.show()

Output:

cos()

The cos() method of the math module returns the cosine of the given angle.

Syntax:

math.cos(x)

• x is the input angle. x must be a number.

The cos() method returns a floating-point value ranging from -1 to 1. If the input value is given in degrees, it must be converted to radians.

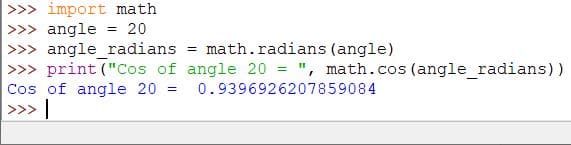
Code:

import math
angle = 20
angle_radians = math.radians(angle)
print("Cos of angle 20 = ", math.cos(angle_radians))

Output:

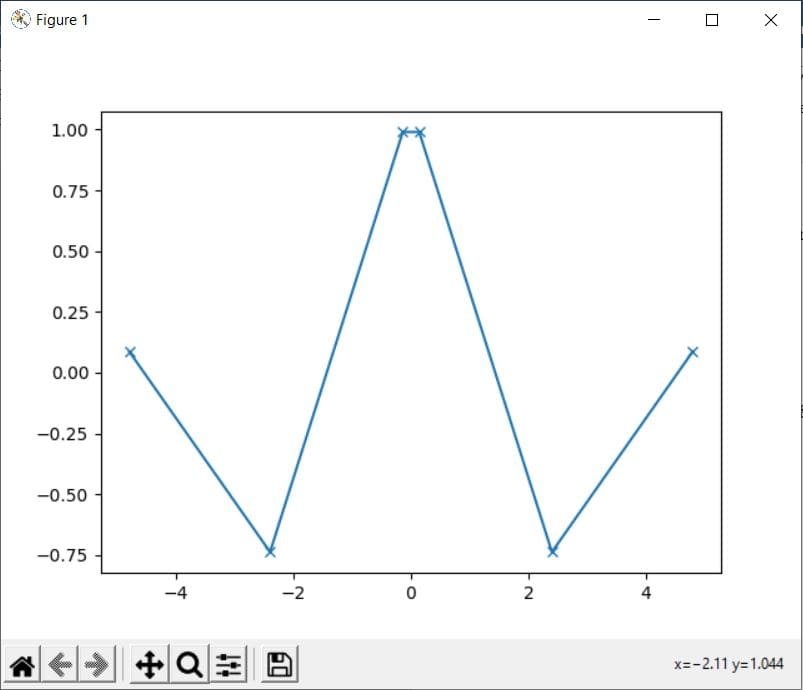
Consider the following example in which we will plot the values from the cos() method on a graph:

Code:

import math
import matplotlib.pyplot as plt
x = [-4.8, -2.4, -0.14, 0.14, 2.4, 4.8]
y = []
for i in range(len(x)):
	y.append(math.cos(x[i]))
plt.plot(x, y, marker = "x")
plt.show()

Output:

tan()

The tan() method of the math module returns the tangent of the given angle.

Syntax:

math.tan(x)

• x is the input angle. x must be a number.

The tan() method returns a floating-point value. If the input value is given in degrees, it must be converted to radians.

Code:

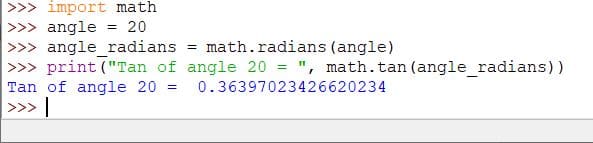
import math
angle = 20
angle_radians = math.radians(angle)
print("Tan of angle 20 = ", math.tan(angle_radians))

Output:

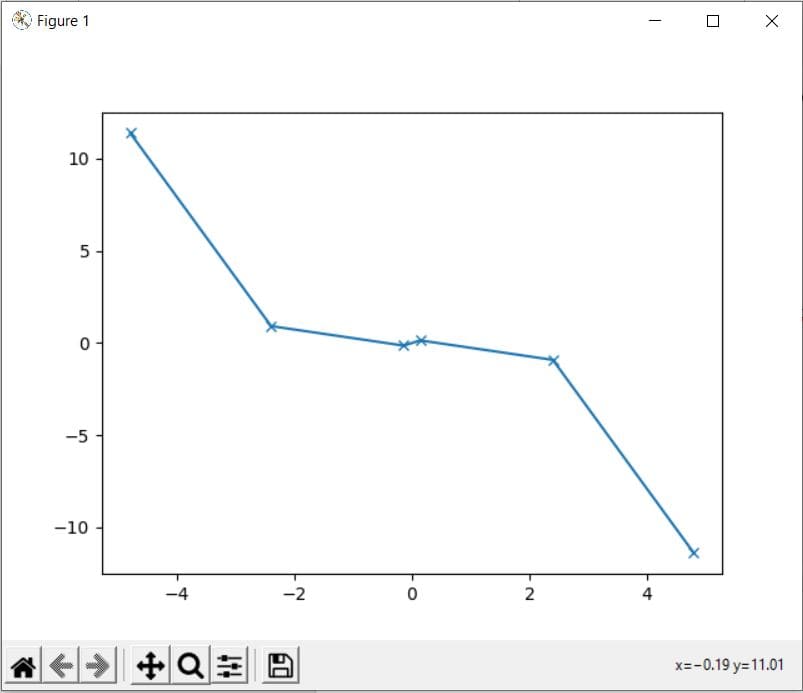
Consider the following example in which we will plot the values from tan() method on a graph:

Code:

import math
import matplotlib.pyplot as plt
x = [-4.8, -2.4, -0.14, 0.14, 2.4, 4.8]
y = []
for i in range(len(x)):
	y.append(math.tan(x[i]))
plt.plot(x, y, marker = "x")
plt.show()

Output:

sinh()

The sinh() method of the math module finds the hyperbolic sine of an angle.

Syntax:

math.sinh(x)

• x is the input angle. x must be a number.

The sinh() method returns a floating-point value. If the input value is given in degrees, it must be converted to radians.

Code:

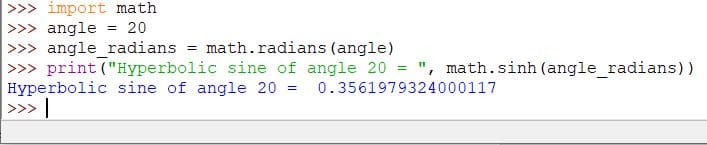
import math
angle = 20
angle_radians = math.radians(angle)
print("Hyperbolic sine of angle 20 = ", math.sinh(angle_radians))

Output:

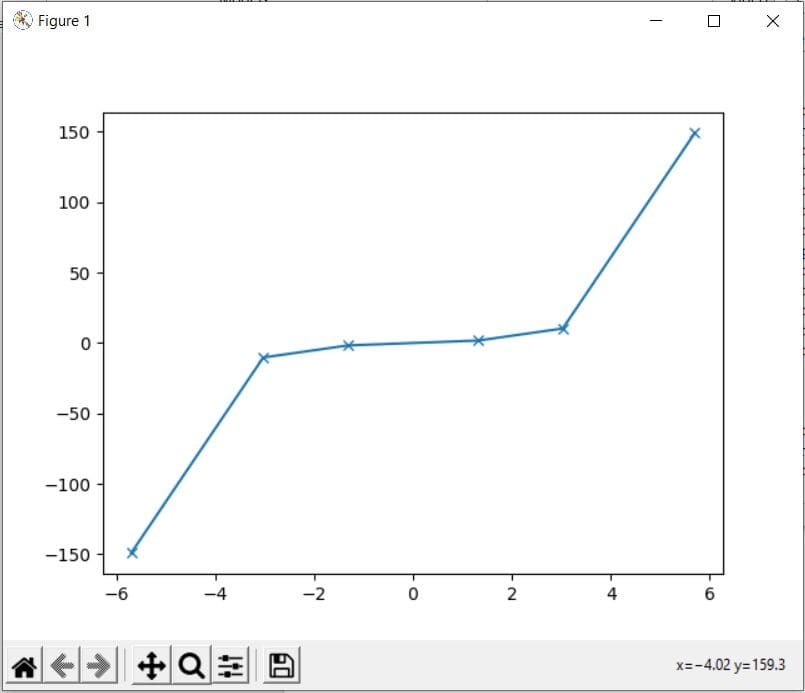
Consider the following example in which we will plot the values from sinh() method on a graph:

Code:

import math
import matplotlib.pyplot as plt
x = [-5.698, -3.028, -1.318, 1.318, 3.028, 5.698]
y = []
for i in range(len(x)):
	y.append(math.sinh(x[i]))
plt.plot(x, y, marker = "x")
plt.show()

Output:

cosh()

The cosh() method of the math module finds the hyperbolic cosine of an angle.

Syntax:

math.cosh(x)

• x is the input angle. x must be a number.

The cosh() method returns a floating-point value. If the input value is given in degrees, it must be converted to radians.

Code:

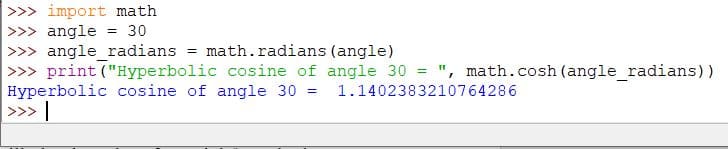
import math
angle = 30
angle_radians = math.radians(angle)
print("Hyperbolic cosine of angle 30 = ", math.cosh(angle_radians))

Output:

Consider the following example in which we will plot the values from cosh() method on a graph:

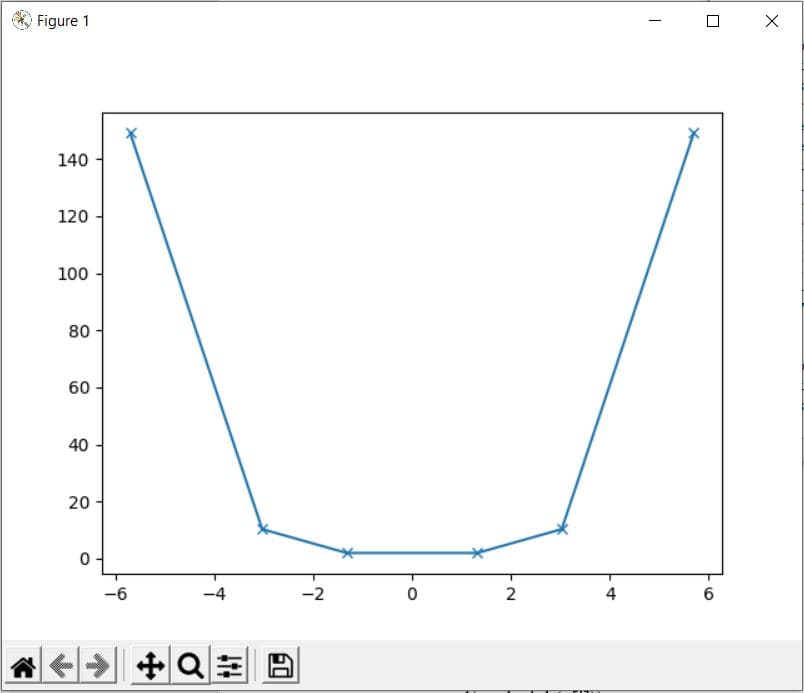
Code:

import math
import matplotlib.pyplot as plt
x = [-5.698, -3.028, -1.318, 1.318, 3.028, 5.698]
y = []
for i in range(len(x)):
	y.append(math.cosh(x[i]))
plt.plot(x, y, marker = "x")
plt.show()

Output:

asin()

The asin() method of the math module finds the arcsine of an angle in radians.

Syntax:

math.asin(x)

• x is the input angle. x must be a number. x should be within the range of -1 to 1.

The asin() method returns a floating-point value.

Code:

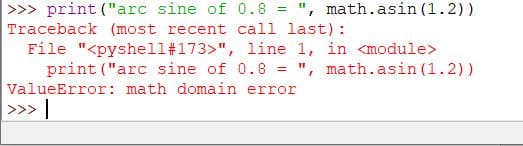
import math
print("arc sine of 0.8 = ", math.asin(0.8))

Output:

If x is greater than 1, you will get an error as shown below:

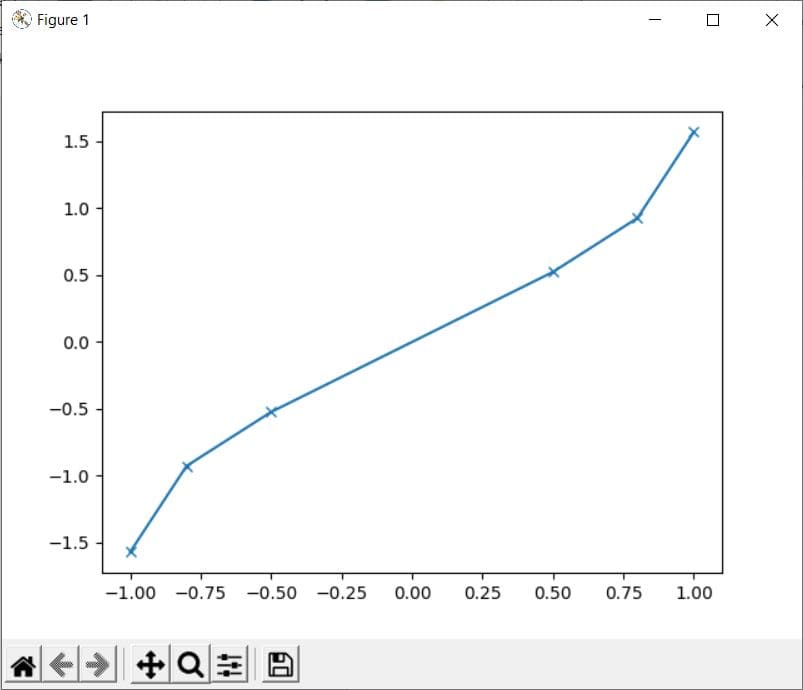
Consider the following example in which we will plot the values from asin() method on a graph:

Code:

import math
import matplotlib.pyplot as plt
x = [-1, -0.8, -0.5, 0.5, 0.8, 1]
y = []
for i in range(len(x)):
	y.append(math.asin(x[i]))
plt.plot(x, y, marker = "x")
plt.show()

Output:

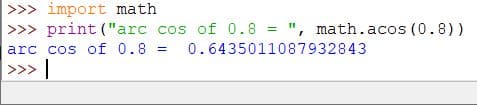
acos()

The acos() method of the math module finds the arccosine of an angle in radians.

Syntax:

math.acos(x)

• x is the input angle. x must be a number. x should be within the range of -1 to 1.

The acos() method returns a floating-point value.

Code:

import math
print("arc cos of 0.8 = ", math.acos(0.8))

Output:

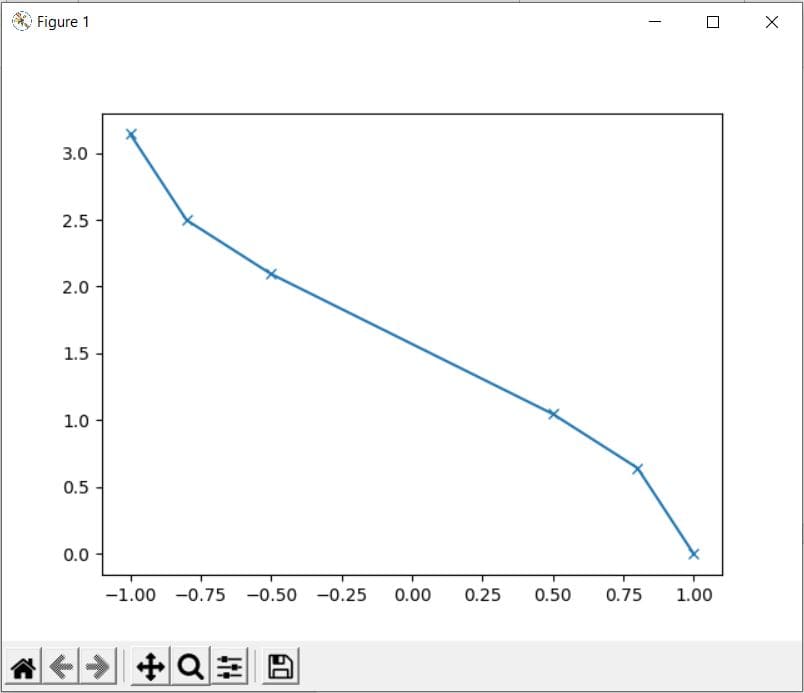
Consider the following example in which we will plot the values from acos() method on a graph:

Code:

import math
import matplotlib.pyplot as plt
x = [-1, -0.8, -0.5, 0.5, 0.8, 1]
y = []
for i in range(len(x)):
	y.append(math.acos(x[i]))
plt.plot(x, y, marker = "x")
plt.show()

Output:

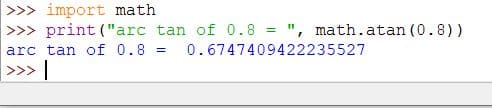
atan()

The atan() method of the math module finds the arctangent of an angle in radians.

Syntax:

math.atan(x)

• x is the input angle. x must be a number.

The atan() method returns a floating-point value ranging from -pi/2 to pi/2.

 

Code:

import math
print("arc tan of 0.8 = ", math.atan(0.8))

Output:

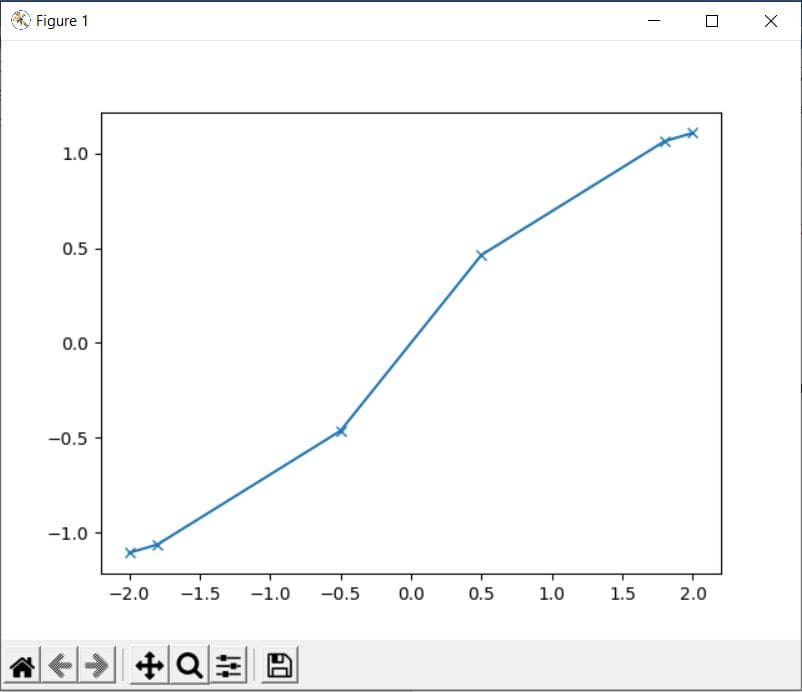
Consider the following example in which we will plot the values from atan() method on a graph:

Code:

import math
import matplotlib.pyplot as plt
x = [-2, -1.8, -0.5, 0.5, 1.8, 2]
y = []
for i in range(len(x)):
	y.append(math.atan(x[i]))
plt.plot(x, y, marker = "x")
plt.show()

Output:

I hope you find the tutorial useful. Keep coming back.

 

Reference:

https://docs.python.org/3/library/math.html