Boost Your Python Code with LRU Cache

LRU Cache, or “Least Recently Used” Cache, is a type of cache where the least recently used entries are discarded when the cache reaches its size limit.

The key idea is to make subsequent requests for the same data faster by reusing the previous results. This technique is called memoization.

In this tutorial, we will explore its underlying mechanism, how to implement it in Python using the functools.lru_cache decorator, and even how to create a disk-based LRU cache for larger applications.

 

 

The functools.lru_cache Decorator

Python provides a built-in LRU cache decorator functools.lru_cache in the functools module, which provides the memoization capability. Let’s apply it to the Fibonacci function:

import functools

@functools.lru_cache(maxsize=128)
def fib(n):
    if n < 2:
        return n
    return fib(n-1) + fib(n-2)
print(fib(10))

Output:

55

The @functools.lru_cache(maxsize=128) is a decorator that wraps our function, enabling it to remember or cache the result of the function calls.

The maxsize parameter is used to specify the maximum size of the cache.

 

Customizing Maximum Size

You can use the maxsize parameter of functools.lru_cache decorator which allows you to customize the maximum number of entries in the cache in case you want to increase the size of the cache:

@functools.lru_cache(maxsize=1024)
def fib(n):
    if n < 2:
        return n
    return fib(n-1) + fib(n-2)
print(fib(100))

Output:

354224848179261915075

Here, we’ve increased the maxsize to 1024.

This allows the fib function to remember more previous function calls. Use this parameter wisely. A larger cache size will use more memory.

If maxsize is set to None, the cache can grow indefinitely.

 

Implementing an LRU Cache from Scratch

We can manually implement an LRU cache using a combination of a Python dictionary and a doubly linked list.

The dictionary will act as the cache while the doubly linked list will keep track of the order of elements.
Let’s start by defining a Node class for our doubly linked list:

class Node:
    def __init__(self, key, value):
        self.key = key
        self.value = value
        self.prev = None
        self.next = None

Next, let’s define our LRU Cache. The LRUCache class will initialize the cache and its size.

The get and put methods will handle retrieval and insertion of items in the cache, respectively.

class LRUCache:
    def __init__(self, capacity: int):
        self.cache = dict()
        # dummy nodes
        self.head = Node(0, 0)
        self.tail = Node(0, 0)
        self.head.next = self.tail
        self.tail.prev = self.head
        self.capacity = capacity

    def get(self, key: int) -> int:
        if key in self.cache:
            node = self.cache[key]
            self._remove(node)
            self._add(node)
            return node.value
        return -1

    def put(self, key: int, value: int) -> None:
        if key in self.cache:
            self._remove(self.cache[key])
        node = Node(key, value)
        self._add(node)
        self.cache[key] = node
        if len(self.cache) > self.capacity:
            node = self.head.next
            self._remove(node)
            del self.cache[node.key]

    def _remove(self, node):
        p = node.prev
        n = node.next
        p.next = n
        n.prev = p

    def _add(self, node):
        p = self.tail.prev
        p.next = node
        self.tail.prev = node
        node.prev = p
        node.next = self.tail

Here, we implemented the LRU Cache where each item in the cache is a node in the doubly linked list. The _remove(node) method removes a node from the list and the _add(node) method adds a node to the end of the list.

When the cache is full (exceeds capacity), the least recently used item (head of the list) is removed.

 

Insertion/retrieval logic

In an LRU cache, items are inserted into the cache as key-value pairs, similar to a dictionary. Upon each insertion, the cache checks whether it is full.

If the cache is full, it removes the least recently used item before inserting the new item. This insertion operation is O(1).
For data retrieval, when a particular key is accessed, the cache moves the accessed key-value pair to the end of the cache as it is the most recently used item.

The retrieval operation is also O(1).
Let’s illustrate this using our manually implemented LRU cache:

# Initialize our cache with the capacity of 2
lru_cache = LRUCache(2)

# Insert some items
lru_cache.put(1, 'a')  # cache is {1='a'}
lru_cache.put(2, 'b')  # cache is {1='a', 2='b'}
print(lru_cache.get(1))  # return 'a'

# This will make the key 1 as recently used so cache will be {2='b', 1='a'}
lru_cache.put(3, 'c')  # Removes key 2 and insert a new entry. Now cache is {1='a', 3='c'}
print(lru_cache.get(2))  # returns -1 (not found)

Output:

a
-1

As we can see, the cache is storing and retrieving data efficiently while maintaining the least recently used order.

 

Popping logic

The popping logic determines which item to remove when the cache is full. In an LRU cache, this would be the least recently used item.

The trade-off of this strategy is that it requires keeping track of what was recently used, but it has the benefit of making sure that as long as an item is frequently accessed, it will remain in the cache.
In our LRUCache implementation, the _remove(node) method handles the popping logic.

When the cache capacity is exceeded, it removes the node next to the head node (i.e., the least recently used node). let’s illustrate the popping logic:

# Continuing from our previous example
lru_cache = LRUCache(2)

# Insert some items
lru_cache.put(1, 'a')  # cache is {1='a'}
lru_cache.put(2, 'b')  # cache is {1='a', 2='b'}
lru_cache.put(3, 'c')  # Removes key 1 (least recently used) and insert a new entry. Now cache is {2='b', 3='c'}

print(lru_cache.get(1))  # returns -1 (not found as it is popped out)
print(lru_cache.get(2))  # return 'b'

Output:

-1
b

As shown, when the cache reached its maximum capacity, it popped out the least recently used item, which was the item with key 1.

When we tried to get the value for the key 1, it returned -1 indicating the item is not found in the cache.

 

Persistence of LRU Cache (Disk-based LRU Cache)

Normally, the data stored in an LRU cache is on memory and gets wiped out when the program finishes its execution.

You can use the Python’s diskcache module to save the LRU cache on disk. Here’s a basic example:

from diskcache import Cache
cache = Cache('my_cache_directory')

@cache.memoize()
def fib(n):
    if n < 2:
        return n
    return fib(n-1) + fib(n-2)
print(fib(10))

Output:

55

In this example, we are using the diskcache.Cache class to create a persistent disk-based cache.

The @cache.memoize() decorator works just like functools.lru_cache, but it stores the cache data on the disk, allowing it to persist between program runs.

 

Thread Safety

The functools.lru_cache decorator is thread-safe. This means that it can be used in a multi-threaded program without the need for locks or other synchronization methods.

import functools
import threading

@functools.lru_cache(maxsize=128)
def fib(n):
    if n < 2:
        return n
    return fib(n-1) + fib(n-2)

def print_fib(n):
    print(f"Thread {n}: {fib(20)}")

threads = []
for i in range(5):
    t = threading.Thread(target=print_fib, args=(i,))
    threads.append(t)
    t.start()

for t in threads:
    t.join()

Output:

Thread 0: 6765
Thread 1: 6765
Thread 2: 6765
Thread 3: 6765
Thread 4: 6765

In the above example, multiple threads can safely call the memoized fib function concurrently.

Each thread prints the 20th Fibonacci number, calculated using our fib function.

 

Performance Analysis

Let’s use the Python time module to compare the execution time of the fib function with and without the LRU cache:

import time
import functools

def fib_no_cache(n):
    if n < 2:
        return n
    return fib_no_cache(n-1) + fib_no_cache(n-2)

@functools.lru_cache(maxsize=128)
def fib_with_cache(n):
    if n < 2:
        return n
    return fib_with_cache(n-1) + fib_with_cache(n-2)

# Calculate time taken by fib_no_cache
start = time.time()
fib_no_cache(30)
end = time.time()
print(f"Without cache: {end - start} seconds")

# Calculate time taken by fib_with_cache
start = time.time()
fib_with_cache(30)
end = time.time()
print(f"With cache: {end - start} seconds")

Output (may vary based on system):

Without cache: 0.6722159385681152 seconds
With cache: 5.0067901611328125e-05 seconds

As you can see, the fib function with LRU cache is significantly faster than without cache.

This clearly demonstrates the performance benefit of using an LRU cache.

 

Profiling and Monitoring LRU Cache

Python’s built-in cProfile module can be used to measure the cache hit/miss rate and its impact on performance.

Moreover, the functools.lru_cache decorator provides some useful statistics that we can use for monitoring the cache’s performance.
Here’s a small example that demonstrates this:

import cProfile
from functools import lru_cache
import time

# Implement a slow Fibonacci function with a small delay
@lru_cache(maxsize=None)
def slow_fib(n):
    time.sleep(0.01)  # a delay of 0.01 seconds
    if n < 2:
        return n
    return slow_fib(n-1) + slow_fib(n-2)

# Define a function to call slow_fib() for a range of numbers
def test_slow_fib(n):
    for i in range(n+1):
        slow_fib(i)

# Use cProfile to profile the test_slow_fib() function
profiler = cProfile.Profile()
profiler.runcall(test_slow_fib, 50)

# Print the profiling results
profiler.print_stats()
print("\nCache Info:", slow_fib.cache_info())

Output:

         104 function calls in 0.796 seconds

   Ordered by: standard name

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
        1    0.001    0.001    0.796    0.796 lru_cache.py:14(test_slow_fib)
       51    0.002    0.000    0.795    0.016 lur_cache.py:6(slow_fib)
       51    0.793    0.016    0.793    0.016 {built-in method time.sleep}
        1    0.000    0.000    0.000    0.000 {method 'disable' of '_lsprof.Profiler' objects}

Cache Info: CacheInfo(hits=98, misses=51, maxsize=None, currsize=51)

The time.sleep function, which we used to introduce a delay, was also called 51 times and took up almost all of the total time.

The cache info tells us that there were 98 cache hits and 51 cache misses.

Visualize cache statistics

We can visualize cache statistics using the matplotlib library to understand how the cache hits grow.
We’ll enhance our function to record cache statistics at each recursive call:

from functools import lru_cache
import matplotlib.pyplot as plt

@lru_cache(maxsize=None)
def fib(n):
    if n < 2:
        return n
    return fib(n-1) + fib(n-2)

# Run the function for a range of numbers and record the number of cache hits and misses after each call
cache_hits = []
cache_misses = []
for i in range(51):
    fib(i)
    info = fib.cache_info()
    cache_hits.append(info.hits)
    cache_misses.append(info.misses)

# Plot the cache hits and misses
plt.figure(figsize=(10,6))
plt.plot(cache_hits, label='Cache Hits')
plt.plot(cache_misses, label='Cache Misses')
plt.xlabel('Fibonacci Input')
plt.ylabel('Count')
plt.legend()
plt.title('LRU Cache Hits and Misses for Fibonacci Numbers')
plt.show()

Output:

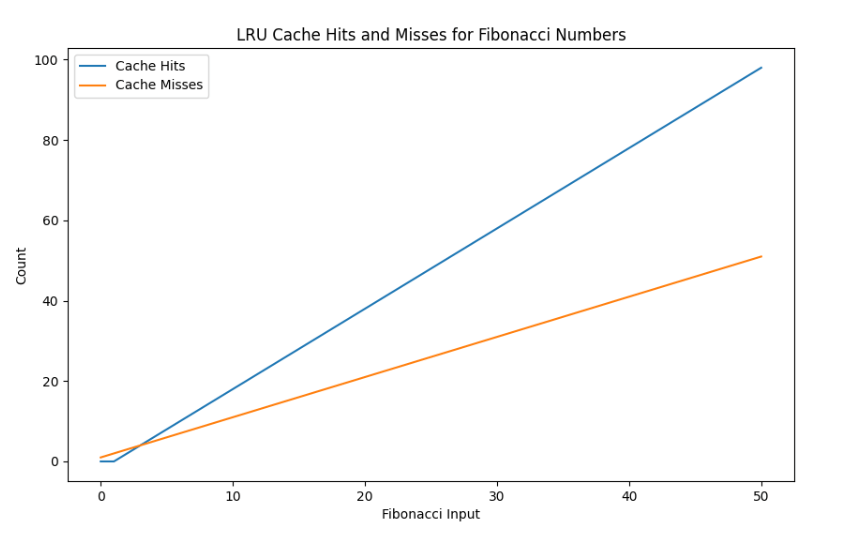
In this code, we record cache_info() at each recursive call to the fib function, storing the results in the cache_hits and cache_misses list.

We then plot the number of cache hits and misses over the course of these calls.
The plot will show the number of cache hits and misses for each recursive call to the fib function.

As you can see, the number of cache hits grows over time, while the number of cache misses levels off, indicating that our cache is effectively reducing the number of redundant calculations.

 

Real-world Use Cases of LRU Cache

LRU caches can optimize many real-world applications.

Here’s a simple example of how you might use lru_cache for database query optimization:

import functools
import sqlite3

@functools.lru_cache(maxsize=1024)
def get_employee_details(db_path, emp_id):
    conn = sqlite3.connect(db_path)
    cursor = conn.cursor()
    cursor.execute("SELECT * FROM employees WHERE id=?", (emp_id,))
    details = cursor.fetchall()
    conn.close()
    return details

# employee.db is our database and it has a table 'employees'
details = get_employee_details('employee.db', 123)

In the above example, when you fetch the details of an employee, it caches the result.

The next time you fetch the details for the same employee id, it will return the result from the cache instead of querying the database again.

 

Limitations and Drawbacks of LRU Cache

While LRU cache provides a simple and effective strategy for cache management, it’s not without its limitations:

1. Space Usage: If not limited, an LRU cache will grow indefinitely with each unique request. It’s crucial to set an appropriate size for the cache to ensure efficient memory usage.
2. Cache Stampede: A cache stampede can occur when multiple threads attempt to read a value from the cache that has just been popped. This can cause high load and significantly degrade performance.
3. Ineffectiveness for certain data access patterns: If the data access pattern is such that each request is unique or updated frequently, an LRU cache will not be effective because it will not be able to serve any request from the cache.

Alternatives to LRU Cache:

1. Least Frequently Used (LFU): An LFU cache pops out the least frequently used items first. This can be more efficient than an LRU cache if frequently accessed items are also frequently updated.
2. Random Replacement (RR): A simple strategy that randomly selects a candidate item for eviction. This can be effective if the access pattern is completely random.
3. Segmented LRU (SLRU): This is an extension of LRU, which has two LRU lists (a probationary segment and a protected segment), providing a better hit ratio than a plain LRU cache.

 

Further Reading

https://docs.python.org/3/library/functools.html