A Foolproof Guide to Infinity In Python

We often encounter and have to deal with infinity in many real-world scenarios, and so we need a way to represent them in programming languages.
In this tutorial, we’ll learn how to represent and work with infinity in Python.

 

 

What is Infinity?

Before diving into the programming know-how of working with infinity, let us first understand what infinity is, by formally defining it

There are dozens of definitions of infinity depending on its usage in different contexts and domains. We’ll focus on the ones that are used in mathematics and computing.
Infinity is defined as a large, ‘undefined’ number that is bigger than any real number.
It exists on both ends of the number line, and hence we have both positive and negative infinities.
Infinity is denoted using the symbol ∞.

In Computer Science, it is also defined as a result of an ‘undefined operation’ such as division by zero. In programming, infinity is used to define an absolute max/min value in algorithms defined for optimizations.

 

How to Write Infinity using float?

We can declare infinity as a floating-point number, by passing the string value ‘inf’ or ‘infinity’ to the method float.

a = float("inf")
print(f"value of a = {a}")
print(f"type of a = {type(a)}")

Output:

As we discussed, there also exists ‘negative infinity’. We can declare the same by passing ‘-inf’, or by creating positive infinity, and prefixing it with ‘-‘ sign.

b = float("-inf")
print(f"value of b = {b}")
print(f"value of -float('inf') = {-float('inf')}")

Output:

Note that the string that we pass to the float method is case-independent. So passing “INF” or “inFINIty” would also be correctly evaluated to inf.

 

Why the infinity is float type?

You must be wondering why the infinity is not int type, and if it’s an undefined number how does its datatype matter?

The answer lies in the way the numbers are represented in Python.
An integer number is represented using its binary representation, for eg. 5 is represented as 0101.
The floating-point numbers, on the other hand, are represented using 3 components – sign, mantissa, and exponent. This is as per the IEEE 754 standard for storing floating-point numbers.

The IEEE 754 standard reserves some values to represent special numbers. One of these special numbers is infinity.
According to this standard, a floating-point number represents an infinity when all the bits in the exponent part are 1, and all the bits in the mantissa part are 0.
Additionally, if the sign bit is 0, it is positive infinity, while a 1 in the sign bit denotes a negative infinity.

So, since infinity is a special value that cannot be represented using simple binary representation, hence its datatype is float in Python.

 

Using the Math Module

We can also use Python’s math module to represent infinity.
The module has a predefined value math.inf that can be assigned to variables to represent infinity.

import math
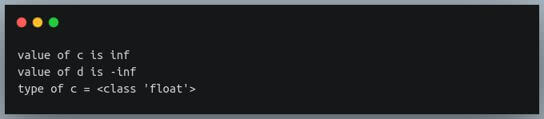
c = math.inf
d = -math.inf #negative inf
print(f"value of c is {c}")
print(f"value of d is {d}")
print(f"type of c = {type(c)}")

Output:

It turns out the math module also defines infinity as a floating-point number and apparently, the infinities declared by the two methods are equivalent.
Let’s check it out.

float_inf = float("inf")
math_inf = math.inf
print(f"float_inf == math.inf is {float_inf == math.inf}")

Output:

 

Checking for Infinity

You can use the math.isinf() to check for infinity like this:

import math
positive_infinity = float('inf')
negative_infinity = float('-inf')
print(math.isinf(positive_infinity)) # returns True
print(math.isinf(negative_infinity)) # returns True

Note that the math.isinf returns true whether the infinity is positive or negative.

 

Using the Decimal Module

Python’s decimal module provides support for fast correctly rounded decimal floating-point arithmetic.

It also provides a way to represent infinity using the Decimal class.
Here’s how you can represent positive and negative infinity using Python’s decimal module:

from decimal import Decimal
positive_infinity = Decimal('Infinity')
negative_infinity = Decimal('-Infinity')

Output:

print(positive_infinity)
print(negative_infinity)

Infinity
-Infinity

In this example, ‘Infinity’ and ‘-Infinity’ are string arguments passed to the Decimal constructor. Python’s decimal module interprets these string arguments as positive and negative infinity respectively.

 

Arithmetic Operations on infinity

Since infinity is a floating-point number, we can perform various arithmetic operations on it, and the results of such operations are also defined by the IEEE standard.

Addition

If we add any finite real number to infinity, the result will be infinity.
If we add infinity to infinity, the result will again be an infinity.
However, if we add a negative infinity to positive infinity, the result will be undefined or NaN (Not a Number). NaN is another special number like infinity that is represented in Python using float datatype, as per IEEE 754 standard.

inf = float("infinity")
print(f"inf + 100  = {inf + 100}")
print(f"inf + 0.52  = {inf + 0.52}")
print(f"inf + inf  = {inf + inf}")
print(f"-inf + inf  = {-inf + inf}")

Output:

Subtraction

Subtracting a positive, real number from infinity yields infinity.
Subtracting infinity from any positive, real number returns negative infinity.
Subtracting infinity from infinity results in an undefined result i.e NaN (as was observed in the previous section).
Subtracting infinity from negative infinity gives negative infinity.

print(f"inf - 50 = {inf - 50}")
print(f"299.9 - inf = {299.9 - inf}")
print(f"inf - inf = {inf - inf}")
print(f"-inf - inf = {-inf - inf}")

Output:

Multiplication

The multiplication of any positive number with infinity gives infinity as the result.
Multiplying infinity by another infinity also results in infinity.
Multiplying infinity by zero is undefined, it returns NaN.
Multiplying infinity by negative infinity, or any negative number, yields negative infinity.

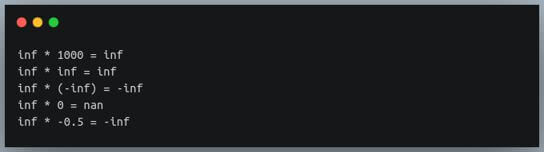
print(f"inf * 1000 = {inf * 1000}")
print(f"inf * inf = {inf * inf}")
print(f"inf * (-inf) = {inf * (-inf)}")
print(f"inf * 0 = {inf * 0}")
print(f"inf * 0.5 = {inf * 0.5}")

Output:

Division

Dividing infinity by any positive or negative number returns positive or negative infinity, respectively.
Dividing infinity by itself, or by negative infinity returns a NaN.
Dividing any finite number by infinity results in 0 or −0.

Finally, dividing infinity by 0 results in ‘ZeroDivisonError’

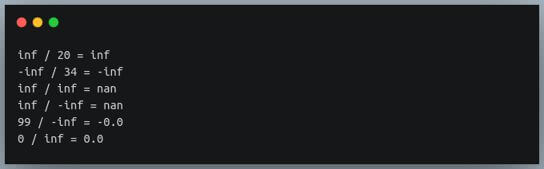
print(f"inf / 20 = {inf / 20}")
print(f"-inf / 34 = {-inf / 34}")
print(f"inf / inf = {inf / inf}")
print(f"inf / -inf = {inf / -inf}")
print(f"99 / -inf = {99 / -inf}")
print(f"0 / inf = {0 / inf}")

Output:

Note that while doing the decimal division of infinity by any number results in infinity; doing floor division, however, results in NaN.

print(f"inf // 20 = {inf // 20}")

Output:

Modulo operation

The modulo operation on two numbers returns the remainder when integer division is performed between the two.

The behavior of modulo operation on infinity is a bit weird.
While modulo of infinity(both positive & negative) with any number (positive, negative, infinity) yields NaN, modulo of a real number with +infinity, however, returns that number.
Modulo of real number with -infinity, on the other hand, gives -infinity as the result.

print(f" 67 % 5 = {67 % 5}")
print(f"inf % 20 = {inf % 20}")
print(f"-inf % 34 = {-inf % 34}")
print(f"inf % inf = {inf % inf}")
print(f"inf % -inf = {inf % -inf}")
print(f"99 % inf = {99 % inf}")
print(f"99 % -inf = {99 % -inf}")
print(f"0 % inf = {0 % inf}")

Output:

 

NumPy infinity

In addition to the math module, and the float method, an infinity can also be assigned using NumPy’s np.inf constant.

NumPy also follows IEEE 754 standard for storing floating-point numbers, and so the value of np.inf is equal to float("inf") and math.inf. The datatype of np.inf is also float.

NumPy’s infinity constant can also be accessed using several aliases such as np.Infinity, np.Inf, and np.infty.
NumPy also defines separate constants for positive and negative infinities. Positive infinity can be accessed using np.PINF (alias for np.inf), and the negative infinity can be accessed using the constant np.NINF.

import numpy as np
import math
a = np.inf
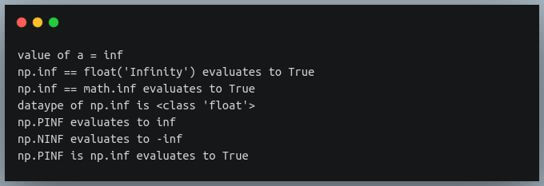
print(f"value of a = {a}")
print(f"np.inf == float('Infinity') evaluates to {np.inf == float('Infinity')}")
print(f"np.inf == math.inf evaluates to {np.inf == math.inf}")
print(f"dataype of np.inf is {type(np.inf)}")
print(f"np.PINF evaluates to {np.PINF}")
print(f"np.NINF evaluates to {np.NINF}")
print(f"np.PINF is np.inf evaluates to {np.PINF is np.inf}") #alias check

Output:

NumPy also has methods to find out whether a value is an infinity or not. It also has separate methods to check if the value is positive or negative infinity.

b = np.inf
print(f"b = {b}")
print(f"np.isinf(b): {np.isinf(b)}")
print(f"np.isposinf(b): {np.isposinf(b)}")
print(f"np.isneginf(b): {np.isneginf(b)}")
c = np.NINF
print(f"\nc = {c}")
print(f"np.isneginf(c): {np.isneginf(c)}")

Output:

Note that we can also pass NumPy arrays to these methods; it will return an array of boolean values, denoting positions in the array where the value is infinity.

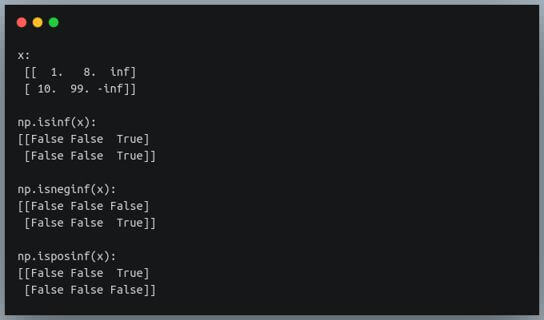
x = np.array([1,8, float("inf"), 10, 99, -math.inf]).reshape((2,3))
print(f"x:\n {x}\n")
print(f"np.isinf(x):\n{np.isinf(x)}\n")
print(f"np.isneginf(x):\n{np.isneginf(x)}\n")
print(f"np.isposinf(x):\n{np.isposinf(x)}\n")

Output:

 

Checking for Positive or Negative Infinity

In some cases, you may want to check if a value is positive infinity or negative infinity specifically. NumPy provides two convenient functions for this: np.isposinf() and np.isneginf().

Here’s an example of how to use these functions:

import numpy as np
positive_infinity = np.inf
negative_infinity = np.NINF
num = 100

print(np.isposinf(positive_infinity)) # True
print(np.isposinf(negative_infinity)) # False
print(np.isposinf(num)) # False

print(np.isneginf(positive_infinity)) # False
print(np.isneginf(negative_infinity)) # True
print(np.isneginf(num)) # False

Conversely, NumPy also has a method called np.isfinite to check if the value is finite or not.

 

Using Pandas with Infinity

Suppose we have a DataFrame with some infinite values, and we want to perform operations on it. Here is an example:

import pandas as pd
import numpy as np
df = pd.DataFrame({
    'A': [1, 2, np.inf],
    'B': [4, -np.inf, 6],
    'C': [7, 8, 9]
})
print(df)

Output:

     A    B  C
0  1.0  4.0  7
1  2.0 -inf  8
2  inf  6.0  9

Pandas provides the function DataFrame.isin() to check for infinite values:

print(df.isin([np.inf, -np.inf]))

Output:

       A      B      C
0  False  False  False
1  False   True  False
2   True  False  False

The isin([np.inf, -np.inf]) function returns a DataFrame of boolean values that indicate whether a value is infinite.

 

Infinity in Algorithms

Infinity is widely used in computer science algorithms, especially in graph-related algorithms like Dijkstra’s algorithm for finding the shortest path.

The concept of infinity is used to initialize distances between nodes because initially, we do not know the distances, so we assume them to be infinite.
Here is a simplified demonstration of how infinity can be used in Dijkstra’s algorithm:

import math

# Suppose we have the following graph represented as an adjacency matrix
graph = {
    'A': {'B': 1, 'C': 4},
    'B': {'A': 1, 'C': 2, 'D': 5},
    'C': {'A': 4, 'B': 2, 'D': 1},
    'D': {'B': 5, 'C': 1}
}

# Dijkstra's algorithm
def dijkstra(graph, start_node):
    shortest_distances = {node: math.inf for node in graph}
    shortest_distances[start_node] = 0  # The distance of the start node from itself is always 0
    unvisited_nodes = list(graph)

    while unvisited_nodes:
        # Select the node with the smallest distance
        current_node = min(unvisited_nodes, key=lambda node: shortest_distances[node])
        unvisited_nodes.remove(current_node)

        for neighbour, distance in graph[current_node].items():
            new_distance = shortest_distances[current_node] + distance
            if new_distance < shortest_distances[neighbour]:
                shortest_distances[neighbour] = new_distance

    return shortest_distances

# Find the shortest distances from node 'A'
shortest_distances = dijkstra(graph, 'A')
print(shortest_distances)

Output:

{'A': 0, 'B': 1, 'C': 3, 'D': 4}

In the above example, Dijkstra’s algorithm finds the shortest path from the start node to all other nodes in the graph.

Initially, the distances to all nodes are set to positive infinity using math.inf because we assume that we don’t know anything about the graph structure.

The start node’s distance is set to 0 as the distance from any node to itself is always 0.

 

Maximum value for infinity

We have discussed that infinity is a ‘large, undefined number’ that is larger than any finite number.
But there are limitations in a computer on the maximum value a variable can store. We cannot declare any large value, and compare it with infinity.

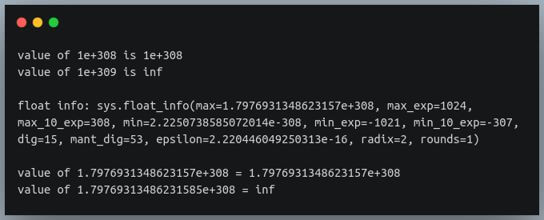
In Python, there is a value between 1e+308 and 1e+309 that is the maximum value that a float variable can store.

The exact value can be found using the attribute sys.float_info.
This displays the various properties of the floating-point datatype on that computer, including the maximum value a float variable can store in Python.
Any value greater than this value is interpreted as infinity.
Similarly, on the negative end, any value below a certain minimum value is interpreted as negative infinity.

print(f"value of 1e+308 is {1e+308}")
print(f"value of 1e+309 is {1e+309}")
import sys
print(f"\nfloat info: {sys.float_info}\n")
print(f"value of 1.7976931348623157e+308 = {1.7976931348623157e+308}")
print(f"value of 1.79769313486231585e+308 = {1.79769313486231585e+308}")

Output:

While we are at it, let us also discuss the behavior of the exponentiation (power) operator on infinity.
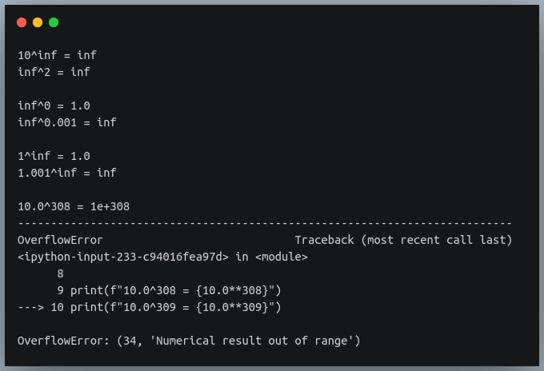
If we try to find any power(except 0) of infinity, or if we calculate the value of any number(except 1) raised to the power infinity, the result will be infinity.
However, if we perform an exponentiation operation using two finite numbers, and if the result exceeds the maximum allowed value, instead of returning infinity as the result, we get an ‘OverflowError’ with the message ‘Numerical result out of range’.

inf = np.inf
print(f"10^inf = {10**inf}")
print(f"inf^2 = {inf**2}\n")
print(f"inf^0 = {inf**0}")
print(f"inf^0.001 = {inf**0.001}\n")
print(f"1^inf = {1**inf}")
print(f"1.001^inf = {1.001**inf}\n")
print(f"10.0^308 = {10.0**308}")
print(f"10.0^309 = {10.0**309}")

Output:

 

Comparing Infinity

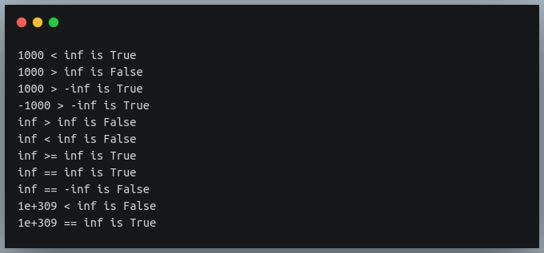
Any number is smaller than +inf. Any number is greater than -inf.
inf is neither smaller nor greater than inf>. It is equal to inf, and not equal to -inf.

inf = float("Inf")
print(f"1000 < inf is {1000 < inf}")
print(f"1000 > inf is {1000 > inf}")
print(f"1000 > -inf is {1000 > -inf}")
print(f"-1000 > -inf is {-1000 > -inf}")
print(f"inf > inf is {inf > inf}")
print(f"inf < inf is {inf < inf}")
print(f"inf >= inf is {inf >= inf}")
print(f"inf == inf is {inf == inf}")
print(f"inf == -inf is {inf == -inf}")
print(f"1e+309 < inf is {1e+309 < inf}")
print(f"1e+309 == inf is {1e+309 == inf}")

Output:

 

Pass infinity as a command-line argument

When we run a Python file from the command line, we can additionally pass any number of arguments we want.
These arguments can be accessed using sys.argv.
sys.argv contains a list of command-line arguments passed to the Python program. The first element in the list is the Python filename, and the remaining elements are the additional values passed (separated by a space) following the filename.

All the values in this list are stored as Python strings.

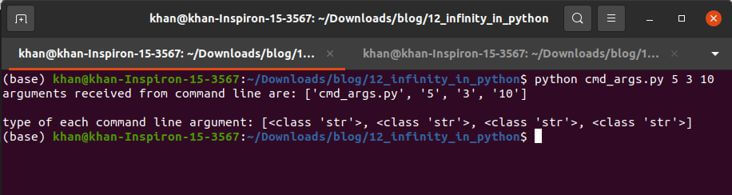
#cmd_args.py
import sys
print(f"arguments received from command line are: {sys.argv}\n")
datatypes = [type(x) for x in sys.argv]
print(f"type of each command line argument: {datatypes}")

Output:

Since all the command-line arguments are received as strings by default, if we want the arguments to be of a certain datatype (eg. float, int, etc.), we need to convert the string arguments into our desired datatype.
In this way, if the user needs to pass ‘infinity’ as one of the arguments, we can convert the same using the float method, and store it in a variable.

Let us take an example where we expect 3 numeric command-line arguments, the first of which is an integer and the remaining ones are float.

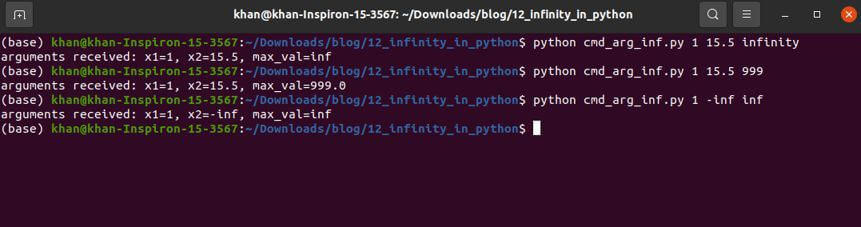
#cmd_arg_inf.py
import sys
arguments = sys.argv[1:]
x1 = int(arguments[0])
x2 = float(arguments[1])
max_val = float(arguments[2])
print(f"arguments received: x1={x1}, x2={x2}, max_val={max_val}")

Output: